Abstract

As real-time embedded vision systems become more ubiquitous, the demand for better energy efficiency, runtime, and accuracy have become vital metrics in evaluating overall performance. These requirements have led to innovative computing architectures, leveraging heterogeneity that combine various accelerators into a single processing fabric. These new architectures lead to new challenges in understanding the most efficient way to partition and optimise algorithms on the most suitable accelerator.

In this thesis, domain-specific optimisation techniques are applied to enhance performance and resource efficiency for image processing algorithms on heterogeneous hardware. Domain-specific optimisations are preferred for being hardware agnostic and their ability to cater to a wider range of image processing pipelines within the domain. First, a literature analysis is conducted on image processing implementations on heterogeneous hardware, high-level synthesis tools, optimisation strategies, and frameworks. The first objective is to develop macro-micro benchmarks for image processing algorithms to determine the suitability of these algorithms on hardware accelerators. The profiling led to the development of a comprehensive benchmarking framework, Heterogeneous Architecture Benchmarking on Unified Resources (HArBoUR). The framework decomposes each algorithm into its fundamental properties that would affect overall performance. A collection of representative image processing algorithms from various operation domains (e.g., Filters, Morphological, Geometric, Arithmetic, CNNs, Feature Extraction ) and full pipelines (e.g., edge detection, feature extraction, convolutional neural network) are used as examples to understand the compute efficiency of on three hardware platforms (CPU, GPU, FPGA).

The results show that parallelism and memory access patterns influence hardware performance. GPUs excel for algorithms with large data-size parallel operations and regular memory access patterns. FPGAs better suit lower parallel factor and data-sized operations. In addition, optimising for irregular memory access patterns and complex computations remains challenging on both FPGA and GPU architectures. However, FPGAs offer high performance relative to their resource and clock speed, but their specialised architecture requires careful implementation for optimal results. In the case of feature extraction algorithms, GPU acceleration is preferable for high matrix operation-intensive stages due to faster execution times. At the same time, FPGAs are more suitable for lower arithmetic stages due to comparable performance and energy consumption profiles. Edge detection and CNN pipelines demonstrate GPUs faster performance but at a significantly higher energy consumption than FPGAs. FPGAs exhibit lower latency than GPUs, considering initialisation and memory transfer times. CPUs perform comparably to both hardware in low-complexity and data-dependant algorithms. In CNN pipelines, FPGAs compute particular layers faster but generally have slower total inference times than GPUs. Nonetheless, FPGAs offer flexibility with bit-widths and operation-fused custom kernels.

Domain-specific optimisations are applied to algorithms such as SIFT feature extraction, filter operations, and CNN pipelines to understand the runtime, energy, and accuracy. Techniques such as downsampling, datatype conversion, and convolution kernel size reduction are investigated to enhance performance. These optimisations notably improve computation time across different processing architectures, with the SIFT algorithm implementation surpassing state-of-the-art FPGA implementations and achieving comparable runtime to GPUs at low power. However, these optimisations led to a 5-20% image accuracy loss across all algorithms.

Finally, the research outcomes described above are applied to two constructed heterogeneous architectures aimed at two domains, low-power (LP) and high-power (HP) systems. Partitioning strategies are explored for mapping CNN layers and operation stages of feature extraction algorithms onto heterogeneous architectures. The results demonstrate that layer-based partitioning methods outperform their fasted homogeneous accelerator counterparts regarding energy efficiency and execution time, suggesting a promising approach for efficient deployment on heterogeneous architectures.

Attestation

I understand the nature of plagiarism, and I am aware of the University’s policy on this.

I certify that this dissertation reports original work by me during my PhD except for the following:

Chapter 4: The results and text are taken from my own ’A Benchmarking Framework for Embedded Imaging’ paper.

Chapter 5: The results and text are from my own ’Domain-Specific Optimisations for Real-time Image Processing on FPGAs’ Journal paper.

Chapter 6: The results and text are from my own ’Energy Aware CNN Deployment on Heterogeneous Architectures’ paper.

Signature: Teymoor Rasheed Ali 29/12/2023

List of Symbols and Acronyms

Acronyms

Acronym	Description
ASIC	Application Specific Integrated Circuit
APU	Application Processing Unit
CNN	Convolution Neural Network
CPU	Central Processing Unit
TPU	Tensor Processing Unit
NPU	Neural Processing Unit
DNN	Deep Neural Network
DSL	Domain-Specific Language
FFT	Fast Fourier Transform
FLOP	Floating Point Operation
FPS	Frames Per Second
FPGA	Field-Programmable Gate Array
GPU	Graphics Processing Unit
HDL	Hardware Descriptor Language
HLS	High-Level Synthesis
IP	Intellectual Property
MSE	Mean Square Error
NPU	Neural Processing Unit
PCIe	Peripheral Component Interconnect Express
ReLU	Rectified Linear Unit
ResNet	Residual Network
RMSE	Root Mean Square Error
RTL	Register-Transfer Level
SIFT	Scale-Invariant Feature Transform
SSD	Solid State Drive
SSIM	Structural Similarity Measure
VHDL	VHSIC Hardware Description Language
VPU	Vision Processing Unit

Statement of Originality

The research conducted within the scope of this thesis produced the following novel and unique contributions towards domain-specific optimisation techniques for image processing algorithms on heterogeneous architectures:

State of the art analysis of literature found within the heterogeneous computing and domain-specific optimisation research domain.

A framework that studies features of image processing algorithms to identify characteristics. These features help partition complex algorithms in determining optimal target accelerators within heterogeneous architectures.

The approach adopts a systemic and multi-layer strategy that offers trade-offs between accuracy within the imaging sub-domains e.g., CNNs and feature extraction. Specifically, HArBoUR enables support in constructing end to end vision systems while providing expected results and guidance.

Domain knowledge-guided hardware evaluation of computational tasks allows imaging algorithms to be mapped onto hardware platforms more efficiently than a heuristic based approach.

Benchmark of representative image processing algorithms and pipelines on various hardware platforms and measure their energy consumption and execution time performance. The results are evaluated to gain insight into why certain processing accelerators perform better or worse based on the characteristics of the imaging algorithm.

Proposition of four domain-specific optimisation strategies for image processing and analysing their impact on performance, power and accuracy;

Validation of the proposed optimisations on widely used representative image processing algorithms and CNN architectures (MobilenetV2 & ResNet50) through profiling various components in identifying the common features and properties that have the potential for optimisations.

Proposal of an efficient deployment of a CNN that is computationally faster and consumes less energy.

Novel partitioning methods on a heterogeneous architecture by studying the features of CNNs to identify characteristics found in each layer which are used to determine a suitable accelerator.

Two heterogeneous platforms which consist of two configurations are developed, one high-performance and the other, power-optimised embedded system.

Benchmarking and evaluating runtime, energy, and inference of popular convolution neural networks on a wide range of processing architectures and heterogeneous systems.

Introduction

The emergence of heterogeneous processor technology has enabled real-time embedded vision systems to become ubiquitous in many applications, such as robotics[1], autonomous vehicles[2], and satellites[3]. Real-time image processing is inherently resource-intensive due to the complex algorithms that demand significant computational power and memory bandwidth. As such, optimising the performance of image processing systems requires a delicate balance between hardware capabilities, software efficiency, and algorithmic innovation to ensure timely and responsive processing. Traditionally, imaging tasks implemented on homogeneous architectures were limited in their adaptability in handling diverse sets of operations. On the contrary, the advent of heterogeneous architectures offers a flexible computing environment that combines multiple accelerators such as CPUs, GPUs, and FPGAs, offering a choice for executing tasks according to their computational requirements.

Integrating such accelerators together poses significant challenges within design and implementation. These challenges are evident in the complexities of scheduling tasks on different hardware units, managing synchronisation, memory coherence, and addressing interconnect requirements. Additionally, the absence of standardised models for heterogeneous systems impacts the programming environment, making it challenging for developers to create cohesive applications. Lastly, performance evaluation becomes a multifaceted task, requiring a comprehensive understanding of the interactions between processing units and their contributions to overall system performance.

However, the primary challenge lies in determining the most effective approach for algorithm partitioning on heterogeneous architectures. Given that each processing architecture executes specific algorithms more efficiently than the other[4], [5]. In addition, navigating an environment with various tool-sets and libraries further compounds the challenge, requiring developers to carefully select and integrate the appropriate tools that align with each processor’s properties. Consequently, partitioned algorithms require further hardware and algorithmic optimisations to extract maximum performance. Typically, domain-specific optimisation techniques are often overlooked limiting the full realisation of performance potential and efficiency gains.

Within the scope of the thesis, the aim is to demonstrate that leveraging heterogeneous architectures for image processing algorithms will increase performance in terms of both runtime and energy consumption. Consequently, this work introduces domain-specific optimisation techniques to further improve application efficiency.

Motivation

The history of the microprocessor can be traced back to 1959 when Fair-child Semiconductors made a significant breakthrough by creating the first integrated circuit. This invention revolutionised the field of electronics by laying the foundation for integrating multiple transistors and other components into a single silicon chip. In the early 1970s, Intel Corporation introduced the first commercially available microprocessor. The Intel 4004[6], released in 1971, was a 4-bit processor capable of performing basic arithmetic and logical operations, with a clock speed of 740 kHz, it represented a significant leap in computing power compared to previous electronic circuits. The 4004 was primarily designed for calculators and other small-scale applications but soon found use in a wide range of devices. Many manufacturers began to contribute and innovate within the microprocessor space. In 1974, Intel released the 8080[7], an 8-bit microprocessor that became highly influential.

Continuing through the 1970s and 1980s, microprocessors advanced rapi-dly, with increasing processing power, efficiency and improved architecture capabilities. The introduction of 16-bit processors, such as the Intel 8086 and Motorola 68000, marked another significant milestone, enabling more complex applications and operating systems. In addition, ARM introduced a new architecture design which used a reduced instruction set paradigm to streamline the execution of instructions. This paved the way for the modern era of computing, with the rise of personal computers and the increasing integration of microprocessors into various devices and industries. In subsequent decades, microprocessors continued to evolve, with advancements in clock speeds, transistor densities, and architectural designs. The transition from 32-bit to 64-bit architectures expanded the memory addressing capabilities and enabled more demanding applications. Multi-core processors emerged in the early 2000s[8], revolutionising computing by enabling parallel processing and significantly improving performance and efficiency.

At around the same time, as CPU processors continued to evolve, two additional specialised architectures emerged to address specific computational needs: GPUs and FPGAs. GPUs were initially designed to handle the complex computations required for rendering high-quality graphics in video games and multimedia applications. However, their parallel processing capabilities and ability to handle large amounts of data made them well-suited for other computationally intensive tasks, such as scientific simulations. On the other hand, FPGAs offer a different approach to computing. Unlike CPUs and GPUs, which are based on fixed instruction sets, FPGAs provide programmable logic that allows users to configure the hardware functionality to suit specific tasks. This flexibility enables FPGAs to be highly optimised for specific applications, such as digital signal processing, data encoding, and real-time processing. FPGAs are particularly valuable in scenarios that require low latency and high throughput, as they can be tailored to perform specific operations with exceptional efficiency.

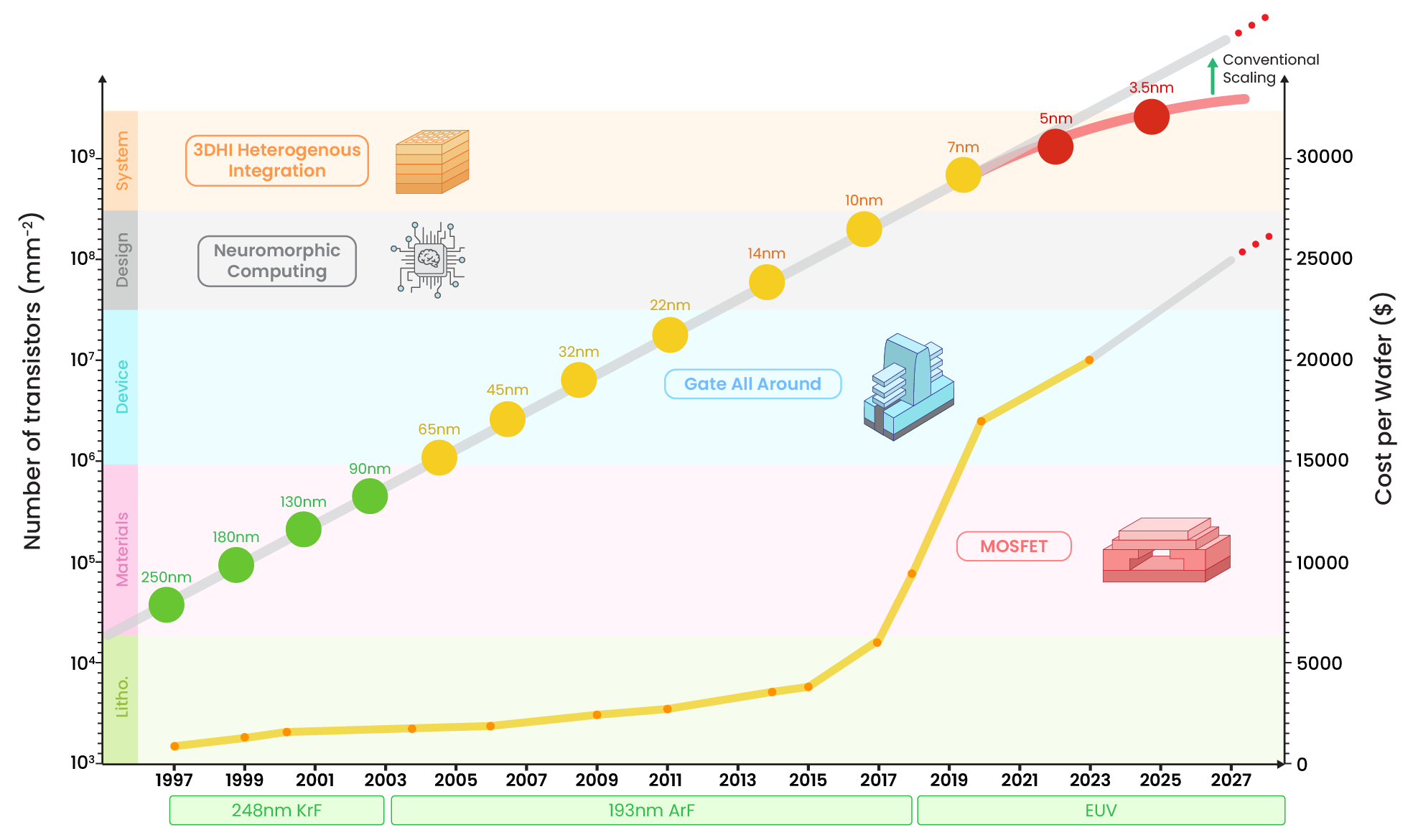
However, in the past decade, processor architecture designs had begun to coalesce, which resulted in a convergence of approaches and a common set of design principles among different CPU manufacturers. As a result, the X86 and ARM instruction sets are the only remaining architectures used in the majority of the systems available. This shift was driven by the realisation that the exponential performance gains seen in previous years were becoming increasingly difficult to achieve due to physical limitations and power constraints, reflected in Fig. 1.1.

The recent emergence of deep learning has reignited the pursuit of specialised computing units, which has fragmented the ecosystem. Developers have started exploring the potential of domain-specific accelerators such as TPUs or NPUs to meet specific computational needs. As a result, the processor landscape has become increasingly diverse again, with different manufacturers pursuing their unique architectural approaches. The growing set of domain-specific accelerators has driven designers to adopt newer and innovative approaches involving heterogeneity. A chiplet-based approach has emerged as a promising paradigm by disaggregating specialised processing units and integrating them into a cohesive interconnected circuit. Each chiplet serves a specific function, leveraging modularity and specialisation to enhance performance, scalability, and customisation. In addition, new packaging methods are utilised to integrate chiplets together, ranging from 2.5D-IC silicon interposers to 3D stacking. Nevertheless, with the deployment of diverse and heterogeneous architectures, a crucial challenge arises in the form of designing algorithms capable of effectively harnessing the capabilities offered by these novel architectural frameworks. This necessitates the development of algorithmic approaches that can optimise performance, exploit parallelism, and efficiently use the unique features and resources provided by these heterogeneous systems.

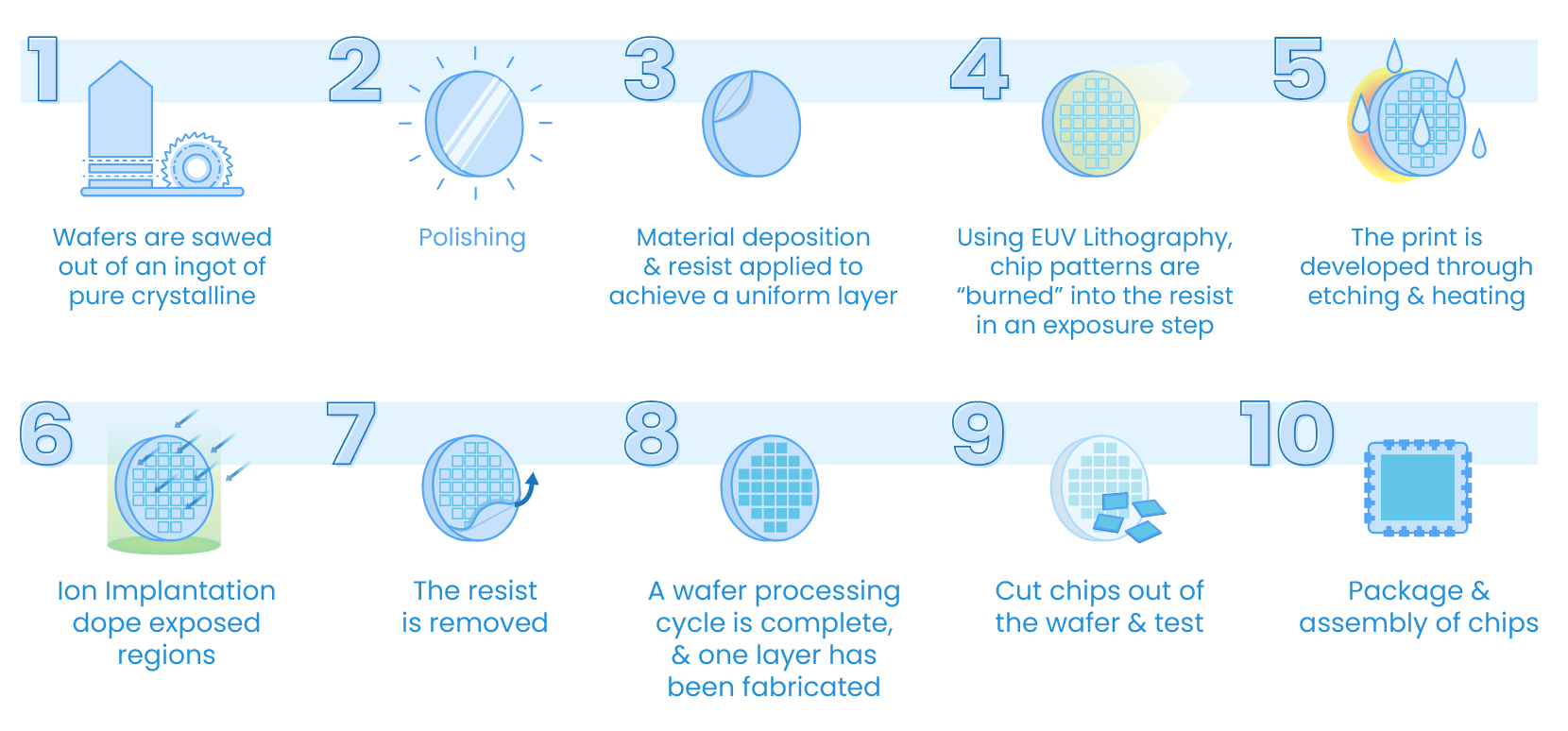
Wafer fabrication, involves a series of steps to transform a silicon wafer into an integrated circuit shown in Fig. 1.2, including wafer preparation, photolithography, etching, layer deposition, and testing for functionality and quality. The pursuit of smaller transistor sizes, driven by demands for enhanced memory capacity and processing capabilities, has led to heavy investment in novel lithography technologies. However, the doubling of transistor densities every two years, as predicted by Moore’s Law, has started to deviate due to technological limitations and economic costs. Shrinking transistors face challenges from the limitations of lithography wavelengths and the increasing complexity of manufacturing processes, leading to lower yields and higher costs. The production of larger silicon wafers has been debated, with the industry transitioning from small diameters in the 1960s to 300mm wafers as the standard by the early 1990s. While larger wafers offer cost and yield benefits, transitioning requires equipment redesign and cost-effectiveness considerations.

In summary, recent years have brought about major changes in the semiconductor industry, driven by the demand from resource intensive algorithms such as image processing and higher wafer fabrication cost. As a result, heterogeneous architectures serve as a potential to increase system performance further. However, understanding how to efficiently partition algorithms on each accelerator and identifying domain-specific optimisation trade-offs remain key challenges in maximising the potential of these architectures.

Research Objectives

This thesis aims to conduct research on partitioning and optimising image processing algorithms on heterogeneous architectures to unlock the full energy and runtime performance. This research encompasses a wide range of multidisciplinary domains (e.g., hardware (CPU/GPU/FPGA), compilers, schedulers, optimisations and programming languages). Therefore, the focus is refined to three primary objectives in this thesis, which are listed in detail below:

Understanding the properties of image processing algorithms and hardware to determine the suitability in order to map operations to the most efficient hardware to increase performance. In addition, exploring optimised tool-sets and libraries in terms of programmability and performance. The goal of this objective is to develop a comprehensive micro/macro bench-marking framework which distils algorithms into their principle operations and gives heuristics towards mapping the operations to correct architecture. Additionally, providing various metrics to evaluate and compare each accelerator. This work enables the partitioning of algorithms on heterogeneous architectures, as realised in later chapters

Investigating domains-specific optimisation techniques which leads to better performance on hardware by exploiting inherent characteristics and structures in the image domain. These optimisations are applied in various combinations to determine the trade-offs in runtime, energy and accuracy metrics. The outcomes of this research enable understanding the efficiency of various hardware-agnostic optimisation methods found within the image processing domain.

Development of a comprehensive heterogeneous platform capable of executing image processing operations across all processing units while efficiently scheduling data for optimal performance. This includes designing and developing two complete heterogeneous platforms for high and low-power applications. Furthermore, using novel layer-wise/stage partitioning techniques on convolutional neural networks and feature extraction algorithms to execute on the most suitable accelerator within the heterogeneous platform. The goal of the objective is to uncover the advantages of heterogeneous architectures in image processing and document their performance gains over single-device solutions.

Thesis Outline

The rest of this thesis is organised as follows:

Chapter 2 presents a technical background on the devices, tools and software deployed in end to end imaging pipelines. This encompasses types of imaging sensors, interfaces, hardware architectures for image processing, high-level synthesis tools and Domain Specific Languages, followed by general discussions of their advantages and drawbacks within the image processing domain.

Chapter 3 critically discusses the state-of-the-art in current literature on optimisations and architectures, which includes HLS/DSL tools, micro/macro benchmarking frameworks and methodologies. Furthermore, an analysis of heterogeneous hardware and their performance in image and domain-specific optimisations.

Chapter 4 presents a novel framework methodology HArBoUR, for heterogeneous architectures which deconstructs image processing pipelines into their fundamental operations and evaluates their performance on hardware platforms, including CPUs, GPUs, and FPGAs. The methodology extends its evaluation to include various hardware based performance metrics, enabling a finer-grained analysis of each architecture’s capabilities.

Chapter 5 presents the proposition of domain-specific optimisations for various imaging and deep-learning algorithms. Each optimisation strategy is applied individually and in combination, and their effectiveness is validated using runtime, accuracy and energy consumption metrics.

Chapter 6 proposes two algorithm types and their implementations on heterogeneous architectures, two convolution neural networks and one feature extraction algorithm. The accuracy, energy consumption and runtimes are recorded and compared to their discrete counterparts.

Chapter 7 concludes this thesis by summarising the research outcomes, i.e., analysis, proposed benchmarking framework and optimisation strategies on heterogeneous algorithms. Novel contributions are highlighted here along with suggestions on new ideas for future research in this domain.

Publications

Journals

Ali, T., Bhowmik, D. & Nicol, R. Domain-Specific Optimisations for Image Processing on FPGAs. Journal of Signal Process Systems (2023). https://doi.org/10.1007/s11265-023-01888-2

Reports

M, Bane, O, Brown, T, Ali, D, Bhowmik, J, Quinn, D, Stansby. ENERGETIC (ENergy aware hEteRoGenEous compuTIng at sCale). https://doi.org/10.23634/MMU.00631226

Under Preparation

Ali, T., Bhowmik, D. & Nicol, R. A Benchmarking Framework for Imaging Algorithms on Heterogeneous Architectures.

Background

In this chapter, the following sections review central components that make up the image processing pipeline. The components are divided into four categories: 1) Image Sensor Type and Characterisation 2) Interface Technologies 3) Hardware Processing Architectures 4) Software Tool-sets. The first category discusses the most common image sensor designs and various noises sources. The second category observes the data transfer performance of each interfaces between the sensor and processing hardware. The third category explores the components of hardware architectures used to execute algorithms. The final category delves into the tools and libraries employed for the ease of implementation.

Image Processing Pipeline

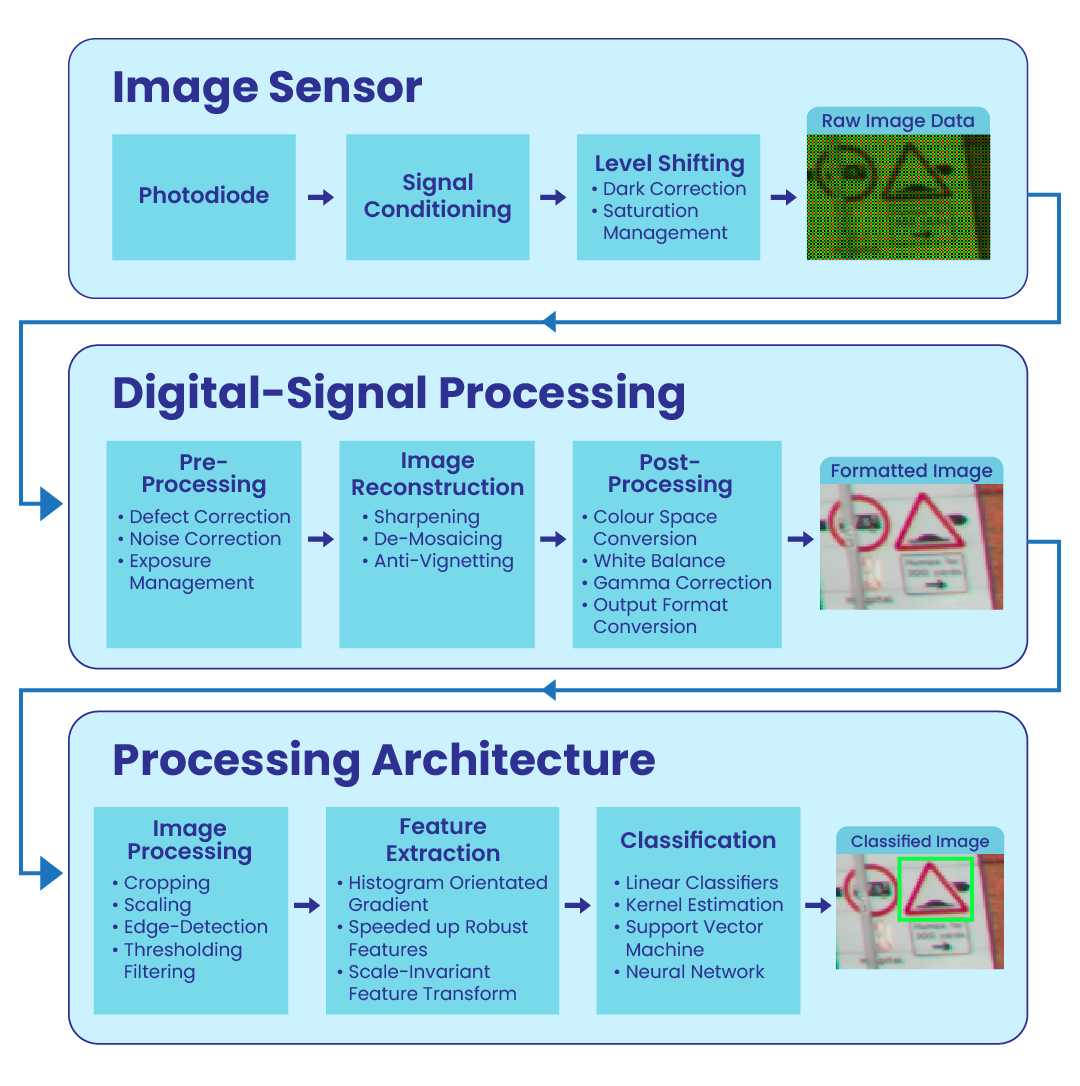
Vision applications fundamentally contain a sequence of operations that form a pipeline shown in Fig. [fig:VisionPipeline]. Firstly, the image sensor captures photons reflected off objects using micro-lens to refract the light into a matrix of wells containing circuits called pixels and the charge produced from the photodiode is converted to a voltage. Once the analogue signal from the image sensor is converted into a digital format, the image data goes through various pixel and frame operations to correct any defects found from the introduction of noise. Furthermore, a full-colour image is reconstructed from the raw frame using a demosaicing algorithm, which may differ depending on the filter pattern e.g., Bayer, X-Trans or EXR. Optionally, the colour image can be compressed into a JPEG format to reduce file size for transmission. The image may contain helpful features that define particular objects, such as shape, colour or texture information. Feature extraction algorithms help identify these characteristics and compile the features into a vector. Finally, a feature vector or image is inputted into a classification algorithm such as a convolution neural network to determine a label or ’class’. The sequence of operations within the pipeline can be reordered or removed to fulfil particular design requirements.

The imaging pipeline comprises various hardware and software components that enable the efficient implementation and execution of image processing algorithms. This chapter presents a complete overview of each component and its limitations. These components include imaging sensors, processing architectures, interface protocols, vision libraries and other tool-sets used to develop a heterogeneous system.

Imaging Sensor

(a) Back-Illuminated	(b) Front-Illuminated

Image sensors are essential components in modern digital imaging devices, such as digital cameras, smartphones, and surveillance systems. These sensors play a crucial role in capturing and converting light into electrical signals, which are then processed to form digital images. Image sensors work on the principle of detecting and measuring light intensity to create a representation of the scene being captured. The most commonly used image sensing technologies within vision systems are charge-coupled device (CCD)[10], and CMOS image sensor(CIS)[11]. CCD technology was developed first and optimised over time for imaging applications, which allowed it to gain a significant market share compared to the newly developed CIS technology, which suffered in image quality due to higher noise. Therefore, CIS sensors were only used in applications where lower cost was the driving factor over image quality. However, over the years, significant advances in silicon size, power consumption, process technology and the reduced fabrication cost of CIS technology resulted in surpassing CCD in market volume. CIS technology can now be found in many applications, from smartphones to medical imaging. Current research on CIS technology focuses on image quality by improving spatial, intensity, spectral and temporal characteristics [12].

Modern image sensors comprise several layers shown in Fig. 2.1 that integrate together to capture and process light. At the topmost layer, microlenses focus incoming light onto the pixel array below, enhancing light sensitivity and overall image quality. Beneath the microlenses lies the pixel array, with each pixel containing a photodiode responsible for converting photons into electric charge. A Bayer pattern colour filter[13], located on top of the pixel array, captures colour information by using red, green, and blue colour filters arranged in a specific pattern. Interpolating algorithms reconstruct the full-colour image from the captured colour data. Wiring and interconnects within the sensor facilitate the efficient transfer of electrical signals from each pixel to the readout circuitry, minimising signal degradation and cross-talk. The silicon substrate forms the foundation for all components, enabling efficient light conversion by the photodiodes and hosting the CMOS circuits for signal processing and readout.

The CCD architecture operates on the principle of transferring charge thro-ugh a sequential shift register. This shift register is a critical component within the CCD chip, responsible for transporting the accumulated charge from each pixel to the output node for further processing. The photons of light strike the pixels of the CCD sensor, which absorbs the incident light, generating an electrical charge proportional to the intensity of the light. The charge in each pixel is horizontally transferred to neighbouring pixels along the shift register. This process, known as "horizontal transfer" in the row direction, uses potential wells to transport charge from one well to the next. After the horizontal transfer, the charge is vertically shifted down the columns. Manipulating voltages in the vertical shift registers moves the charge from one row to the next, guiding it towards the output node. The output node stores the accumulated charge and is connected to an analogue-to-digital converter (ADC) to convert the analogue charge into a digital signal for further processing and storage.

In a CMOS image sensor, the conversion of light into voltage involves several technical steps. Each pixel in the sensor consists of a photodiode, which acts as a light-sensitive capacitor. When incident photons strike the photodiode, it generates electron-hole pairs, and these charge carriers are stored as electric charge in the capacitor. The accumulated charge in each pixel’s capacitor is then transferred to an associated charge-to-voltage conversion circuit, commonly known as the readout circuit. This circuit typically includes a source follower amplifier or a trans-impedance amplifier. The charge is converted into a corresponding analogue voltage signal, proportional to the intensity of the incident light on the pixel. The output voltage from each pixel is then sent to the image sensor’s output circuitry for further signal conditioning and processing. This circuitry may include analogue signal processing components such as analogue filters or amplifiers to enhance the image quality and reduce noise.

In machine vision, the key performance metrics are latency and noise. The differences arise between CMOS and CCD imagers in their signal conversion processes, transitioning from signal charge to an analogue signal and finally to a digital one. In CMOS area and line scan imagers, a highly parallel front-end design enables low bandwidth for each amplifier. Consequently, when the signal encounters the data path bottleneck, typically at the interface between the imager and off-chip circuitry, CMOS data firmly resides in the digital domain. Conversely, high-speed CCDs possess numerous parallel fast output channels, albeit not as massively parallel as high-speed CMOS imagers. As a result, each CCD amplifier requires higher bandwidth, leading to increased noise levels. Therefore, high-speed CMOS imagers exhibit the potential for considerably lower noise compared to high-speed CCDs.

In recent years, semiconductor manufacturers have moved onto stacking imaging sensors depicted in Fig. [fig:3DStacking] to reduce the latency between readout to processing, which was previously developed in the memory domain to increase data storage.

Image Sensor Characterisation

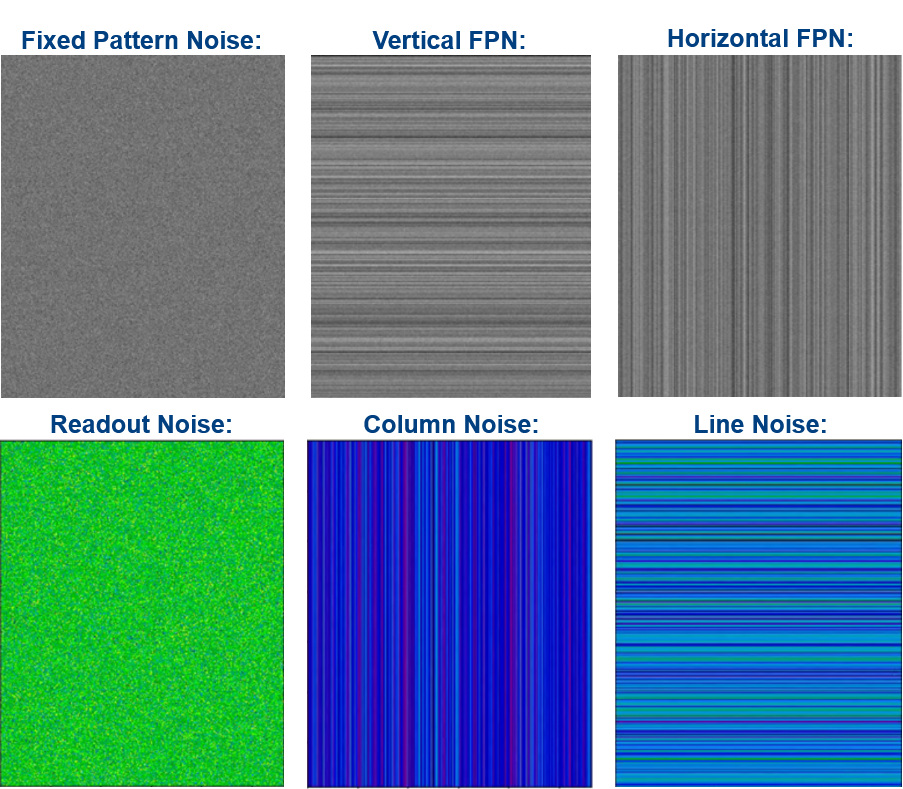
Image sensor characterisation is a process that assesses the performance and capabilities of imaging sensors. The goal is to understand the sensor’s behaviour and limitations to ensure optimal image quality and accurate representation of the captured scene. Noise introduced in sensors come from various sources such as thermal noise, read noise, and photon shot noise, which can degrade image quality, as observed in 2.2. Characterisation involves measuring and analysing these noise components to determine their impact on image fidelity. Noise can be separated into two categories:

Pattern Noise:

This term describes noise patterns that remain constant or fixed over time and across multiple frames or exposures. Fixed pattern noise includes phenomena like Fixed Pattern Noise (FPN), Pixel Non-Uniformity (PRNU), and other systematic and deterministic noise sources.

Random Noise:

The random noise relates to noise that varies over time or across different exposures. It includes sources of noise that exhibit randomness and unpredictability from frame to frame, such as Photon Shot Noise, Readout Noise, Amplifier Noise, and Jitter Noise.

Signal-to-noise ratio (SNR) is a standard metric used to quantify the signal quality captured by the sensor relative to the noise in the image. Dynamic range is another parameter that refers to the sensor’s ability to capture and distinguish details in a scene’s bright and dark regions. A wide dynamic range is essential for preserving details in high contrast scenes without overexposing or underexposing certain areas. Sensitivity and linearity are additional metrics assessed during the characterisation process. Sensitivity determines how well the sensor responds to incoming light, while linearity examines how the sensor’s output corresponds to the actual incident light levels.

Interface Technologies

Vision systems typically rely on input from cameras or other video sources, generating a continuous stream of image frames. Designing algorithms for embedded vision systems requires a detailed understanding of performance and interfacing technologies. The subsequent sections provide an overview of various characteristics related to each technology.

Camera Link

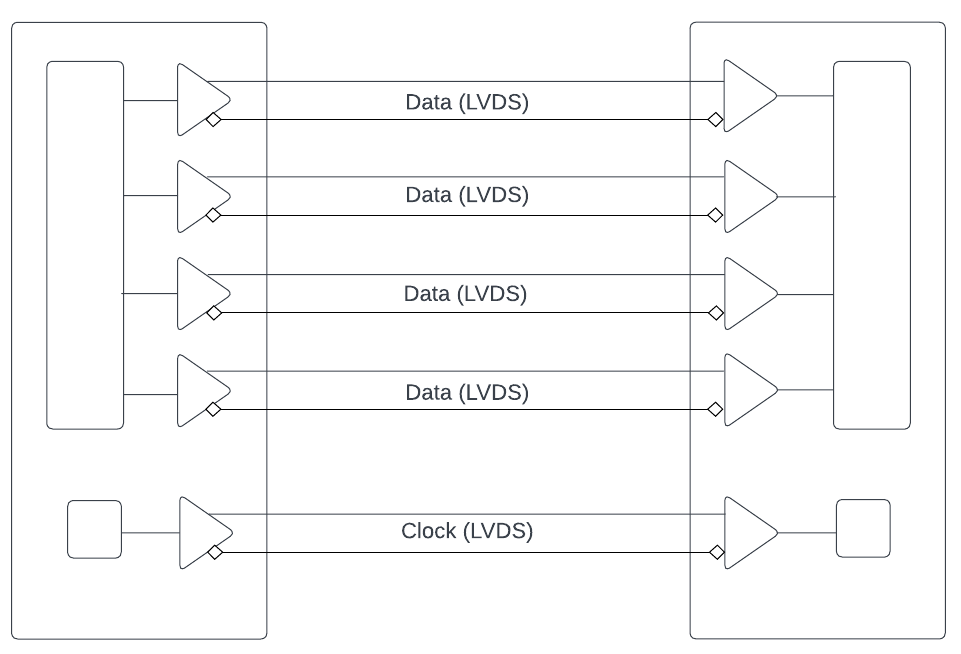
Camera Link[14] is a parallel communication protocol that extends the Channel Link technology and standardises the interface between cameras and frame grabbers. Channel Link provides a one-way transmission of 28 data signals and an associated clock over five LVDS pairs. Among these pairs, one is designated for the clock, while the 28 data signals are multiplexed across the remaining four pairs exhibited in Fig. 2.3, involving a 7:1 serialisation of the input data. A single Camera Link connection allocates 24 bits for pixel data (three 8-bit pixels or two 12-bit pixels) and reserves 4 bits for frame, line, and pixel data valid signals. The pixel clock operates at a maximum rate of 85 MHz. Additionally, four LVDS pairs facilitate general-purpose camera control from the frame grabber to the camera, with the specifics defined by the camera manufacturer. Furthermore, two LVDS pairs are designated for asynchronous serial communication between the camera and frame grabber, supporting a minimum baud rate of 9600 for relatively low-speed serial communication.

For higher bandwidth requirements, the medium configuration includes an additional Channel Link connection, granting an extra 24 bits of pixel data. The full configuration further extends the capacity by incorporating a third Channel Link, resulting in a total of 64 bits of pixel data transmission capability. The versatile nature of Camera Link, with its various configurations, makes it a widely adopted interface standard for high-performance camera systems, particularly in applications demanding real-time image capture and processing.

Peripheral Component Interface Express (PCIe)

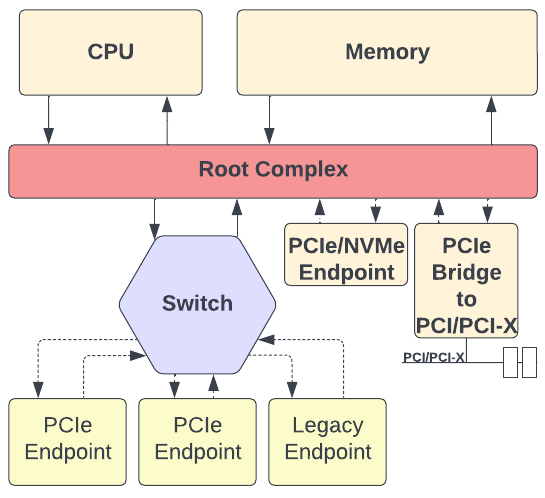
The Peripheral Component Interface Express (PCIe)[15] shown in Fig. 2.4, is an open standard serial bus interface protocol designed in the early 1990s to provide a high-speed interconnect between devices such as Ethernet controllers, expansion/capture cards, storage and graphics processing units. The protocol defined a set of registers within each device known as configuration space, allowing software to view memory and IO resources. In addition, the exposure of peripheral data enables software to assign an address to each device without conflict with other systems. Table [tab:PCIeSummary] summarises each version of the PCIe specification ratified in the past and future.

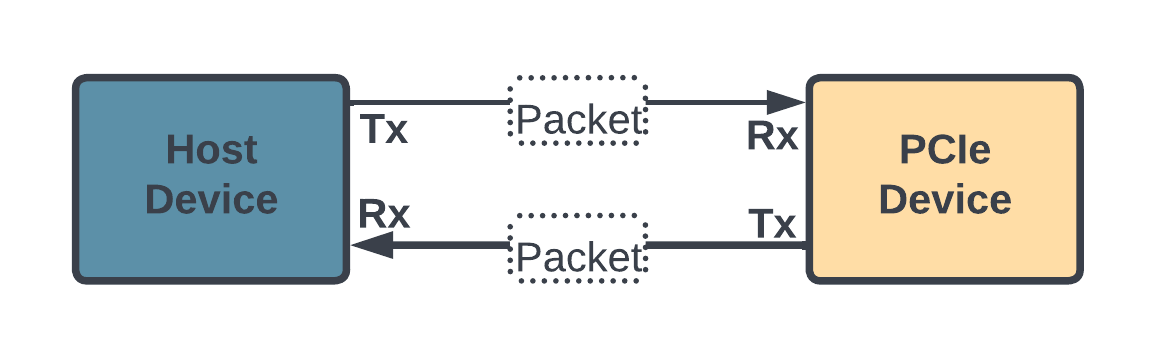
The PCIe architecture consists of a root complex that connects the CPU and memory subsystem to the PCI Express switch fabric composed of one or more PCIe/PCI endpoints. The dual‐simplex connections between endpoints are bidirectional, as shown in Fig. 2.5, which allows data to be transmitted and received simultaneously. The term for this path between the devices is a Link and is made up of one or more transmit and receive pairs. One such pair is called a Lane, and the spec allows a Link to be made up of 1, 2, 4, 8, 12, 16, or 32 Lanes. The number of lanes is called the Link Width and is represented as x1, x2, x4, x8, x16, and x32. The trade‐off regarding the number of lanes to be used in a given design is that having more lanes increases the Link’s bandwidth but at the cost of space requirement and power consumption.

Ethernet

Ethernet technology[16] is based on the Carrier Sense Multiple Access with Collision Detection (CSMA/CD) access method. It operates at the physical layer (Layer 1) and the data link layer (Layer 2) of the OSI model. The physical layer handles the transmission and reception of raw data over the physical medium, while the data link layer is responsible for framing, addressing, and error detection.

One of the main advantages of Ethernet is its flexibility and scalability. It can support various data rates, ranging from 10 Mbps for older versions (e.g., 10BASE-T) to 1 Gbps (Gigabit Ethernet) and beyond for modern implementations. This adaptability allows Ethernet to cater to a wide range of applications, from simple office networks to high-speed data centres and multimedia streaming.

When using Ethernet with FPGAs, designers face the challenge of implementing the higher layers of the OSI model, namely the network layer (Layer 3) and transport layer (Layer 4). These layers are responsible for IP addressing, routing, and end-to-end communication. FPGA designs must include logic to handle IP addressing, packet forwarding, and any higher-level protocols required for data exchange. This complexity can add overhead to the FPGA design and require careful optimisation to ensure efficient data processing.

In FPGA-based systems, the communication between the FPGA and the Ethernet physical layer typically involves a Media Access Control (MAC) core, which is responsible for generating and interpreting Ethernet frames. The MAC core interfaces with the external Ethernet PHY chip, which handles the conversion between the MAC-level signals and the actual physical signals transmitted over the Ethernet cable. In CPU-based systems, handling Ethernet involves the integration of a Network Interface Controller (NIC) or Ethernet controller. The NIC is a hardware component that interfaces the CPU with the Ethernet medium. It manages low-level operations, such as frame reception and transmission, packet encapsulation and decapsulation, and error checking. The NIC communicates with the CPU through driver software that implements higher-level network protocols.

The CPU’s involvement in Ethernet communication extends beyond the data link layer. It handles the network layer protocols (Layer 3), such as Internet Protocol (IP), which involves tasks like IP address assignment, routing, and packet forwarding. Additionally, the CPU manages transport layer protocols (Layer 4), such as Transmission Control Protocol (TCP) and User Datagram Protocol (UDP), responsible for end-to-end communication and data flow control.

GigE Vision

GigE Vision is a standard developed in 2006 by the Automated Imaging Association[17], which extends gigabit Ethernet to transport video data and control information to the camera efficiently. This standard benefits from the widespread availability of low-cost standard cables and connectors, allowing data transfer rates of up to 100 MPixels per second over distances of up to 100 meters.

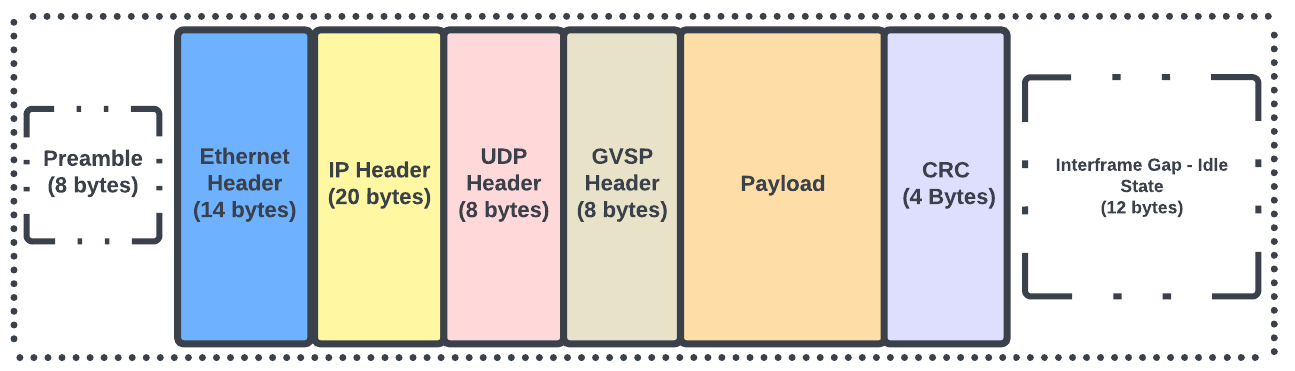
GigE Vision comprises four essential elements. The control protocol facilitates camera control and configuration communication, while the stream protocol governs the transfer of image data from the camera to the host system, both running over UDP. A device discovery mechanism identifies connected GigE Vision devices and acquires their internet addresses. GigE Vision utilises Gigabit Ethernet (1000BASE-T) for data transmission, enabling a maximum data rate of 1 Gbps for real-time transfer of large image and video data in industrial applications. It employs packet-based communication displayed in Fig. 2.6, dividing images into smaller packets for efficient data transfer, ensuring reliable transmission and minimal data loss. Moreover, many GigE Vision cameras support Power over Ethernet (PoE), receiving power through the Ethernet cable, reducing installation overhead. GigE Vision supports both asynchronous and synchronous triggers for precise image capture control. Asynchronous triggers allow continuous image capture at a specified frame rate, while synchronous triggers enable coordinated capture based on external events for synchronised operation with other devices. Additionally, GigE Vision cameras can be easily configured and accessed using the GigE Vision Control Protocol (GVCP), providing efficient camera parameter adjustments and image data retrieval. Overall, GigE Vision is a versatile and efficient interface for industrial imaging applications, offering seamless data transmission and easy camera control.

In many embedded vision applications, it is more practical to integrate the FPGA system within the camera itself, allowing for image processing before transmitting results to a host system using GigE Vision. To achieve real-time operation, a dedicated device driver is used on the host system. This driver bypasses the standard TCP/IP protocol stack for the video stream and employs Direct Memory Access (DMA) transfers to transfer data to the application directly. By avoiding CPU overhead during video data handling, real-time performance can be achieved effectively. This optimised data transfer scheme ensures smooth and efficient communication between the camera and the host system in GigE Vision applications.

Universal Serial Bus (USB)

USB has emerged as a widely used interface for connecting peripheral devices to personal computers. Over the years, USB technology has evolved significantly, supporting increasing link speeds from the initial 1.5 Mb/s and 12 Mb/s to the current 20 Gb/s in the double lane configuration of USB 3.2 Gen 2. As a result, USB has proven to be a viable and versatile interface between FPGAs and SoCs (System-on-Chips) in various applications.

USB operates in a master-slave architecture, where there can be only one host or master controller within a USB network, and the host controller initiates all communication. The communication protocol of USB is structured into four layers: the application and system software interacts with the USB pipe at the topmost layer, while the protocol layer handles packet management. USB packets come in several types, such as Link Management Packets, Transaction Packets, Data Packets, and Isochronous Timestamp Packets. These packets serve to exchange control and status information between the host and the connected devices.

The Data Packet, which carries user data along with a 16-byte header, is essential for transferring information between the host and the device. On the other hand, the other packet types primarily facilitate control and status exchanges. Any data transfer requires initiation by a Transaction Packet before actual data transmission occurs. To enable FPGA access to the USB bus, an external PHY (Physical Layer) chip is necessary. This chip often provides a first-in-first-out (FIFO) interface, which the FPGA can connect to through regular I/O ports. User logic is then required to implement the control logic and interface with the application. While this FIFO interface might limit throughput in certain scenarios, it does not pose any bottleneck for applications like video streaming.

Mobile Industry Processor Interface (MIPI)

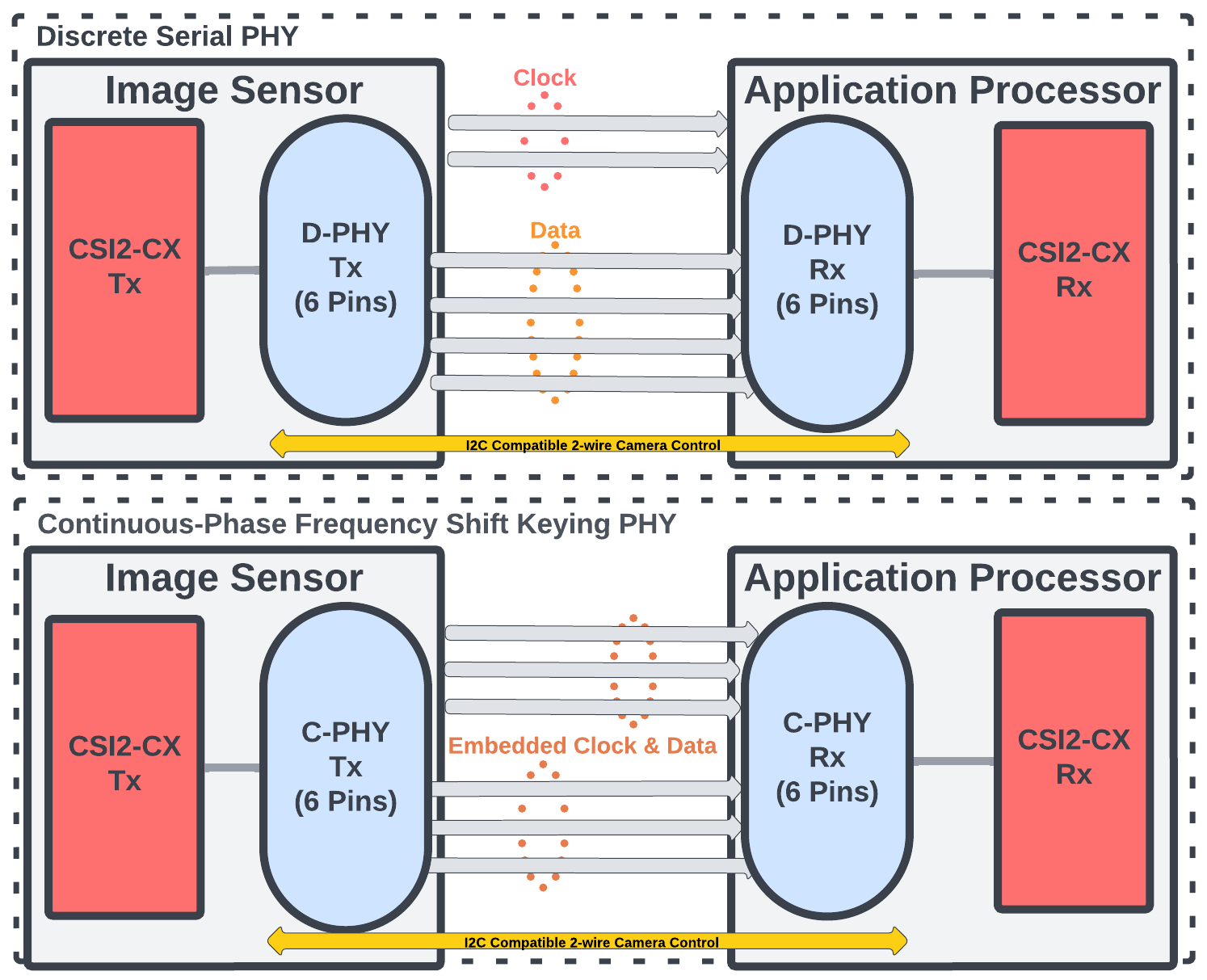
MIPI[18] is a serial interface standard developed in 2003 for interconnecting components in mobile devices. MIPI comes in various versions, and one of the widely used versions in mobile camera interfaces is MIPI CSI-2 (Camera Serial Interface 2). The interface can consist of one or more data lanes, each capable of transmitting a stream of image data. A separate clock lane synchronises the data transmission, ensuring accurate data reception. MIPI CSI-2 supports various data types, including RAW image data and metadata, allowing it to accommodate different image sensor formats and data requirements. Furthermore, the concept of virtual channels enables the multiplexing of multiple data types over the same physical data lanes.

MIPI CSI-2 utilises low-voltage differential signalling to transmit image data from the camera sensor to the application processor. C-PHY and D-PHY are two different physical layer specifications, and their usage depends on the specific requirements of the devices shown in Fig. 2.7. D-PHY provides higher data rates and is capable of reaching extremely high speeds, making it suitable for applications that require substantial data throughput. D-PHY supports multiple data lanes (typically 1 to 4 lanes), and it is commonly used in devices with high-resolution imaging requirements, such as high-end smartphones and cameras. On the other hand, C-PHY, or Combo PHY, is a combination of MIPI C-PHY and MIPI D-PHY technologies. It offers a more power-efficient solution than D-PHY, making it ideal for power-sensitive mobile devices. C-PHY leverages both a low-power, single-ended signalling mode and a high-speed, differential signalling mode, providing a balance between data transfer rates and power consumption. It uses fewer wires compared to D-PHY, simplifying the physical design of mobile devices and potentially reducing costs.

MIPI CSI-2 comes with certain drawbacks that may impact its applicability. Firstly, its physical image data transfer (D-PHY) is limited to shorter cable lengths, typically not exceeding 20 cm, which can be restrictive for certain industrial applications. Additionally, the lack of a standardised plug for MIPI CSI-2 means that sensor/camera modules must be individually and proprietary connected. Moreover, the absence of a standardised driver and software stack requires custom adjustments for each sensor or camera module to work with the CSI-2 driver of a specific System-on-Chip (SoC) through a proprietary I²C driver as a Video4Linux sub-device.

FPGA Mezzanine Card (FMC)

The FMC interface is a high-speed, versatile standard for connecting external modules to FPGAs (Field-Programmable Gate Arrays). The FMC standard encompasses two form factors: single-width and double-width. Single-width supports one connector, while double-width caters to applications needing more bandwidth, front panel space, or larger PCB areas and supports up to two connectors, offering designers flexibility for optimising space and I/O requirements. Two connector types, Low Pin Count (LPC) with 160 pins and High Pin Count (HPC) with 400 pins, displayed in Fig. 2.8. Both support single-ended and differential signalling up to 2 Gb/s, with signalling to an FPGA’s serial connector at up to 10 Gb/s. LPC offers 68 user-defined single-ended signals or 34 differential pairs, along with clocks, a JTAG interface, and optional I2C support for base Intelligent Platform Management Interface (IPMI) commands. HPC provides 160 single-ended signals (or 80 differential pairs), ten serial transceiver pairs, and additional clocks. HPC and LPC connectors use the same mechanical connector, differing only in populated signals, enabling compatibility between them.

Summary

Table [tab:Interfaces] provides a summary of common image sensor interfaces utilised in various imaging applications. These interfaces offer diverse specifications in terms of bandwidth, maximum cable length, frame rate, bit depth, and power consumption, catering to specific imaging needs and requirements. USB4, Thunderbolt and USB offers the highest bandwidth at 40 Gbps while CoaXPress and GigE variants supports the longest cable length at 100 meters which is ideal for distant camera setups. USB provides the highest bit depth options, ensuring better colour precision. MIPI CSI-2 stands out as the most power-efficient interface, consuming only 1.2 W, which is ideal for mobile applications, while CoaXPress requires the most power at 24 W. Although, USB4 can supply up to 240W to cameras or other devices. The only two parallel interfaces are FMC and Cameralink.

Hardware Architectures

In recent years, the demand for flexible, energy-efficient and higher performance processors has continuously grown. This has pushed designers to develop novel processing architectures to facilitate requirements. This section introduces popular processing hardware used within vision applications.

Multi-Core Central Processing Unit (CPU)

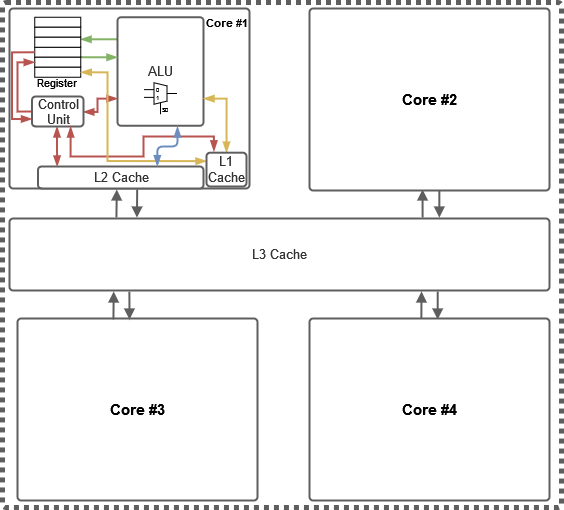
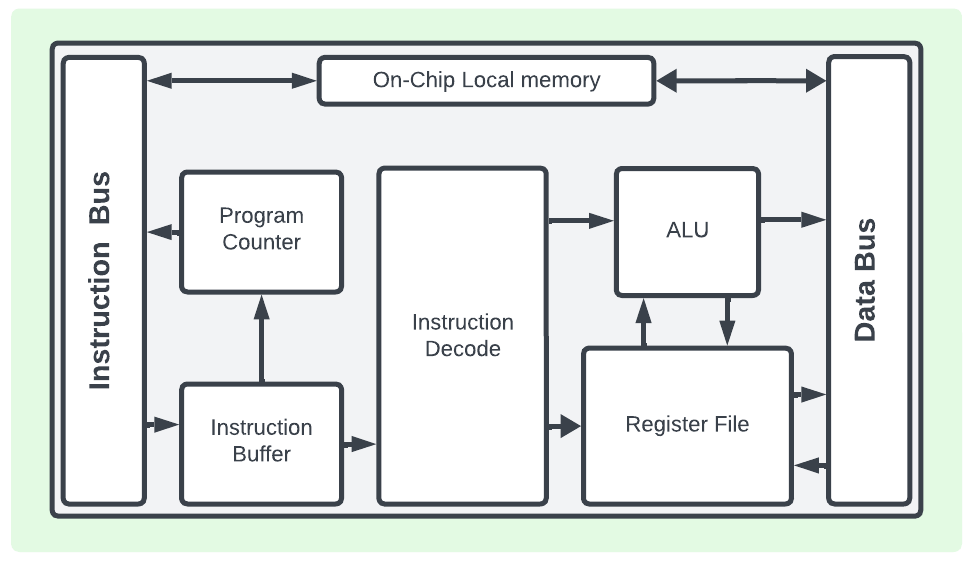
The CPU observed in Fig. 2.9 is an integrated circuit responsible for executing instructions and performing arithmetic, timing, logic and I/O operations. The CPU architecture involves the design and organisation of various components to optimise performance, power efficiency, and instruction execution. The main components are registers, arithmetic logic units (ALUs), control units, cache memory, and instruction pipelines. Registers are small, high-speed storage units within the CPU used for temporarily holding data and intermediate results during computation. ALUs are responsible for performing arithmetic and logic operations, such as addition, subtraction, NOT and OR. The control unit manages the flow of instructions and data within the CPU, fetching instructions from memory, decoding them, and coordinating their execution. CPU cache memory is used to store frequently accessed data, reducing the time taken to retrieve data from main memory.

Reduced Instruction (RISC) and Complex Instruction Set Computer (CISC) are two CPU microarchitecture approaches. RISC architectures prioritise simplicity and efficiency by employing a smaller set of basic instructions. This streamlined design typically leads to faster and more predictable execution, making RISC processors well-suited for power-constrained devices and applications where speed is critical. In contrast, CISC architectures, exemplified by x86, feature a diverse and extensive set of complex instructions designed to reduce the number of instructions required to perform tasks. While this complexity can provide convenience for programmers, it often results in more intricate hardware, potentially impacting performance and energy efficiency.

Significant research is put into improving the execution speed of instruction pipelines. The pipeline breaks down the execution of instructions into multiple stages, allowing different instructions to be processed simultaneously. Each stage of the pipeline handles a specific task, such as instruction fetch, decode, execute, and write back. This pipelining process increases the CPU’s instruction throughput and overall performance. CPU architecture also includes features like branch prediction, speculative execution, and out-of-order execution. Branch prediction predicts the outcome of conditional branches to keep the pipeline filled with useful instructions. Speculative execution allows the CPU to execute instructions before it is confirmed that they are needed, further improving performance. Out-of-order execution enables the CPU to execute instructions in a different order to optimise resource utilisation.

In the past decade, single-core processors have now been outpaced by the shift to multi-core designs. Traditionally, speedup was achieved by increasing the processor’s clock speed and decreasing the transistor size to pack more into the silicon area. However, the power density required grew at a faster rate than the frequency which entailed power problems exacerbated by complex designs attempting to extract extra performance from the instruction stream. This led to designs that were complex, unmanageable, and power-hungry. However, chip designers introduced multiple cores onto a single die and leveraged parallel programming to continue pushing for more performance. The primary advantage to multi-core systems is the raw performance increase from extending the number of processing cores rather than clock frequency, which translates into slower growth in power consumption. This can be a significant factor in embedded devices that operate on a power budget, such as mobile devices.

General-purpose multi-cores are becoming necessary in real-time digital signal processing. One general-purpose core would control various signals and watchdog functions for many special-purpose ASICS as part of a system-on-chip. This is primarily due to the variety of applications and functions required. Nevertheless, multi-Core processors give rise to new problems and challenges. As more processing cores are integrated into a single chip, power and temperature are the primary concerns that can increase exponentially with more cores. Memory and cache coherence is another challenge due to the distributed L1 caches and, in some cases, L2 caches which need to be coordinated.

Graphics Processing Unit (GPU)

The GPU is a specialised hardware architecture initially used for graphics rendering. However, GPUs have undergone significant power and cost advancements, which have captured the attention of both industry and academia. Designers have been exploring the potential of GPUs to accelerate large-scale computational workloads.

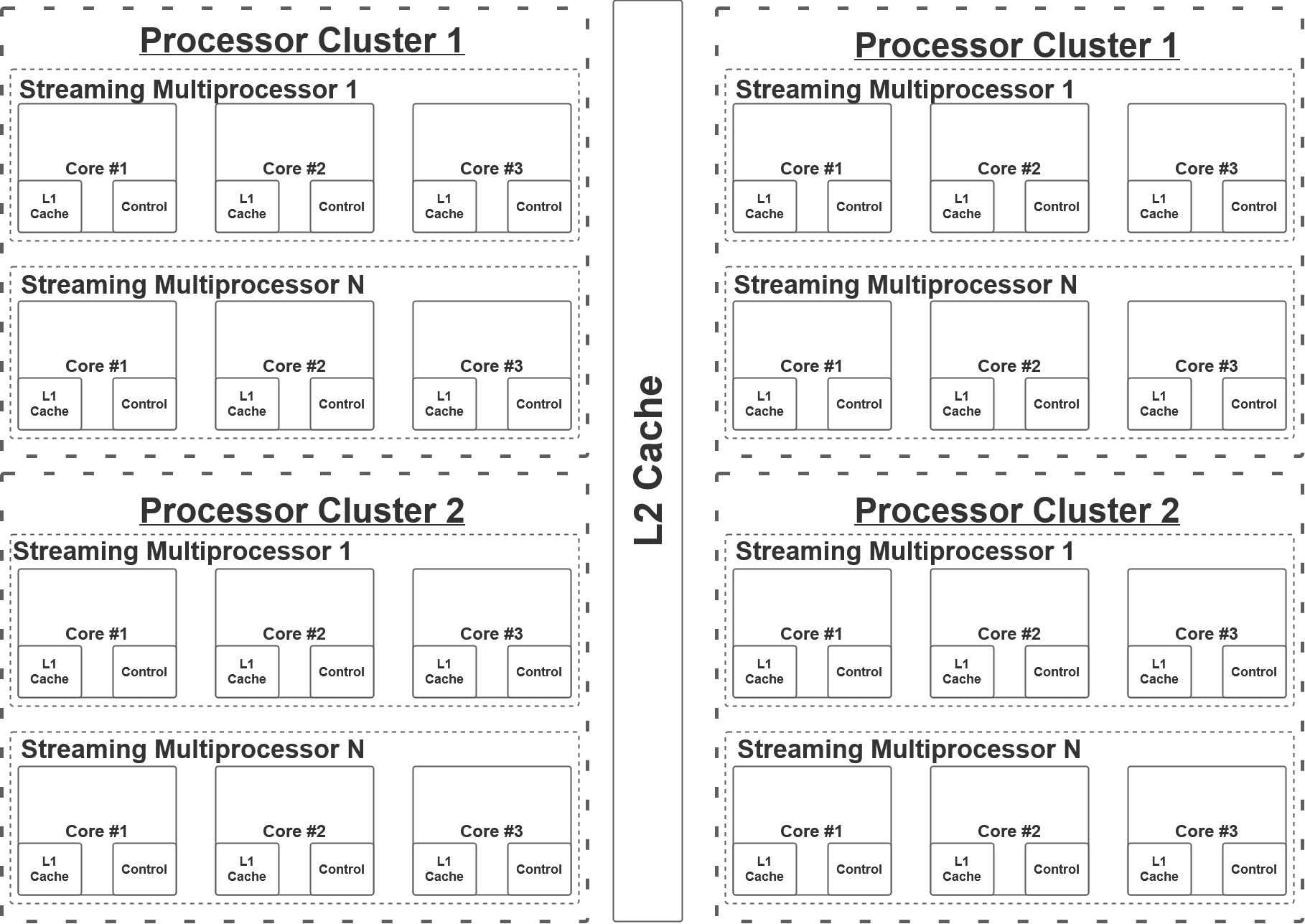
The architecture of GPUs is designed with a focus on throughput optimisation, allowing for efficient parallel computation of numerous operations. Fig. [fig:GPU] illustrates the high-level GPU architecture. The GPU comprises multiple Streaming Multiprocessors (SMs) that function independently, and these SMs are organised into multiple Processor Clusters (PCs). Each SM incorporates a layer-1 (L1) cache with each core. Typically, each SM possesses its dedicated layer-1 cache, and multiple SMs share a layer-2 cache before accessing data from the global GDDR-5 memory. Newer GPU models integrate tensor cores, which efficiently compute matrices calculations, enhancing their performance in deep learning tasks.

The GPU architecture, initially tailored for 3D graphics rendering, involves a streamlined pipeline with distinct stages. It commences with vertex processing, transforming 3D geometric data, followed by primitive assembly to group vertices into primitives. Rasterisation then translates these into screen pixels or fragments, and fragment processing adds attributes like colours and textures. Finally, the pixel output stage writes processed fragments to the frame buffer, resulting in the rendered image on the screen. The highly parallel nature of the graphics pipeline in GPUs makes them exceptionally well-suited for image processing tasks. Image processing often involves manipulating and analysing large amounts of pixel data concurrently, making it a naturally parallelisable task. Leveraging the parallel processing capabilities, image processing algorithms can be accelerated by providing higher frames per second performance for tasks such as image filtering, edge detection, and object recognition. Additionally, GPU optimised memory hierarchy ensures faster access and storage of larger images, kernels and intermediate data.

There remain drawbacks for GPUs, primarily if they are intended to be used as general-purpose machines. Firstly, the limitations of adaptability and context switching make them less suitable for general-purpose computing tasks. Simple calculations which do not utilise the parallelism are inhibited by lower clock speeds. Communication between the CPU and GPU can introduce bottlenecks and decrease the GPU throughput, especially when waiting for results from the CPU. Memory capacity and bandwidth would also affect GPU performance; for example, an image processing application must wait for the image data to be transferred from the main memory, further delaying the runtime. Lastly, GPUs cannot operate independently without support from a CPU, which contributes to more power consumption from idling.

Field-Programmable Gate Array (FPGA)

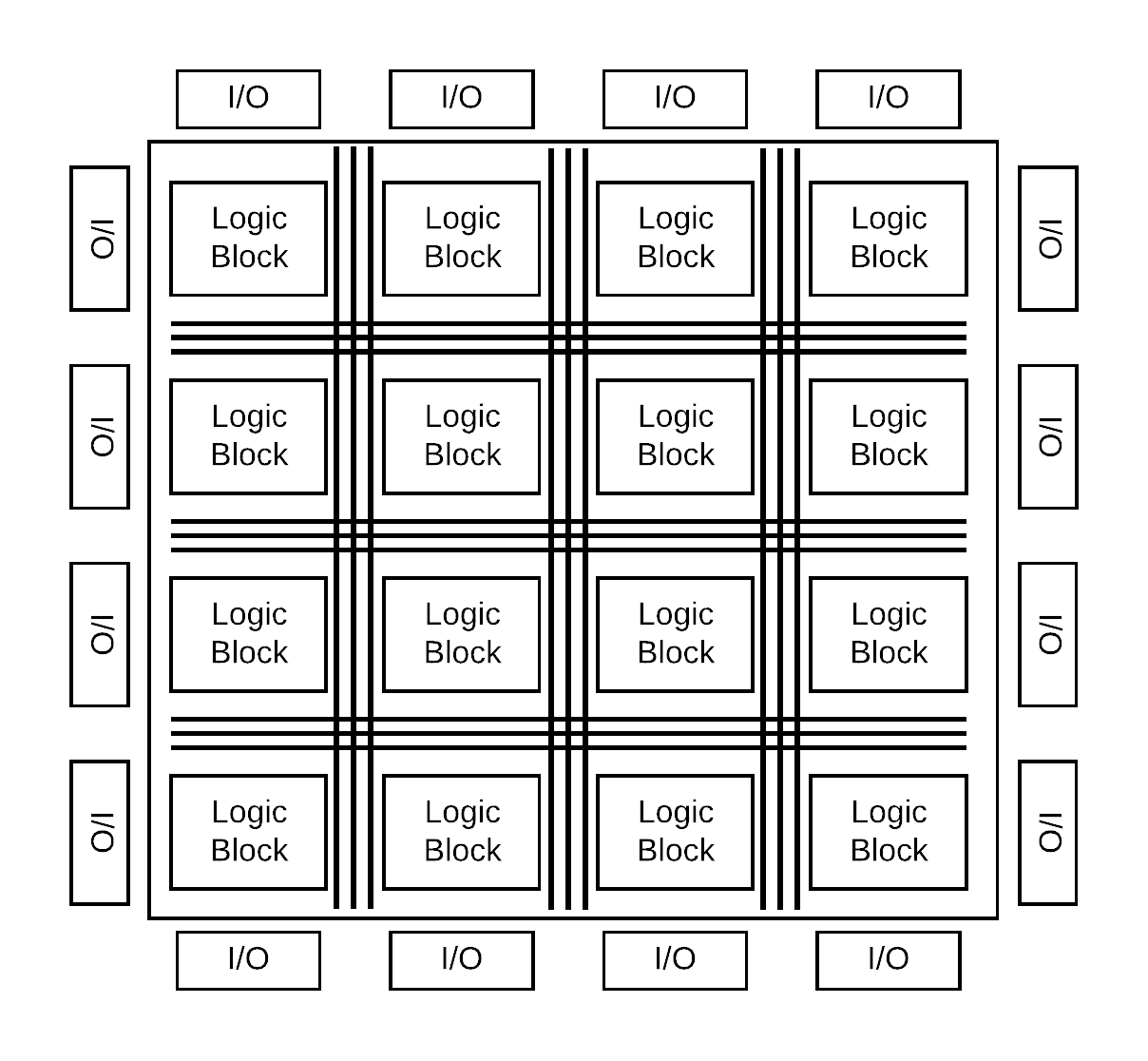
Field-Programmable Gate Arrays are versatile integrated circuits which offer direct hardware programmability for diverse applications. They have gained prominence due to their reconfigurability, making them highly advantageous compared to fixed processing architectures such as ASICs. These features enable shorter time-to-market by allowing prototyping and late-stage design modifications. The FPGA architecture, as depicted in Fig. [fig:FPGA], comprises a matrix of configurable logic blocks (CLBs) containing a combination of look-up tables (LUTs), shift registers (SRs), and multiplexers (MUXs). These components are interconnected through programmable high-bandwidth pathways and are surrounded by I/O ports.

The fine-grained nature of FPGAs empowers designers to exploit both spatial and temporal parallelism in their designs, resulting in enhanced performance. In image processing applications, algorithms can be tailored to operate on individual pixels or groups of pixels in parallel. Temporal parallelism can be achieved using techniques like pipelining, where separate processors work on successive stages of data, allowing concurrent processing and better throughput. Spatial parallelism, however, involves partitioning the image frame and processing each segment independently using separate processors.

FPGAs allow seamless integration of I/O, such as image sensors, enabling pixel data to be streamed directly into processing units without latency. Data can be routed efficiently to other embedded processors without external memory access. Block RAMs (BRAMs) within the FPGA enable exploiting data locality in vision kernels by keeping critical data on-chip. However, the main limitation in image processing applications often stems from external memory (E.g. DDR4 RAM) read/write operations, which can impact overall performance.

Advanced extensible interface (AXI) is a standard protocol for efficient communication between IP blocks within an FPGA design. It follows the Advanced Microcontroller Bus Architecture (ARM AMBA) specification, ensuring compatibility with ARM-based processors and systems-on-chip (SoCs). The AXI protocol supports separate read and write channels, enabling simultaneous data transactions in both directions. It also features burst transfers, allowing multiple data transfers within a single transaction to enhance data throughput.

Despite their advantages, FPGA development requires expertise in hardware descriptor languages (HDL), such as VHDL/Verilog. This steep learning curve can be a challenge for new developers accustomed high-level languages and instruction based architectures. In comparison to ASICs, the support functions and additional reconfigurable logic and power consumption overhead, making power efficiency considerations important during the design phase. FPGAs typically have limited on-chip memory compared to GPUs, which can have limitations for applications that require large memory spaces. Overall, FPGAs offer a powerful platform for image processing tasks, but their effective use requires careful consideration of design constraints and optimisation strategies.

Application-Specific Integrated Circuits (ASICs)

ASICs are a specialised type of Very Large Scale Integration (VLSI) technology where integrated circuits are designed specifically for a particular application domain. This involves custom designing at the transistor level to optimise the circuit for performance and silicon area. There are several advantages of opting for an ASIC implementation over other general-purpose accelerators. The custom designed nature of ASIC logic allows designers to create tightly integrated applications, resulting in better performance, reduced power consumption, and minimised silicon usage. ASICs come with intrinsic trade-offs listed below:

Fixed Design: ASICs are designed for specific applications and lack flexibility compared to general-purpose processors. Once fabricated, it is challenging and costly to make modifications or upgrades to their functionality.

High Design Cost: Designing and prototyping involves significant expertise and time, leading to higher initial development costs.

Long Development Timeline: Creating a custom ASIC requires extensive expertise and significant time to design, verify, and manufacture.

Despite these drawbacks, the per-chip manufacturing cost becomes significantly lower during mass production, rendering ASICs more economically viable for high-volume production. The following sections discuss the various types of ASICS targeting specific workloads:

Vision Processing Units (VPUs)

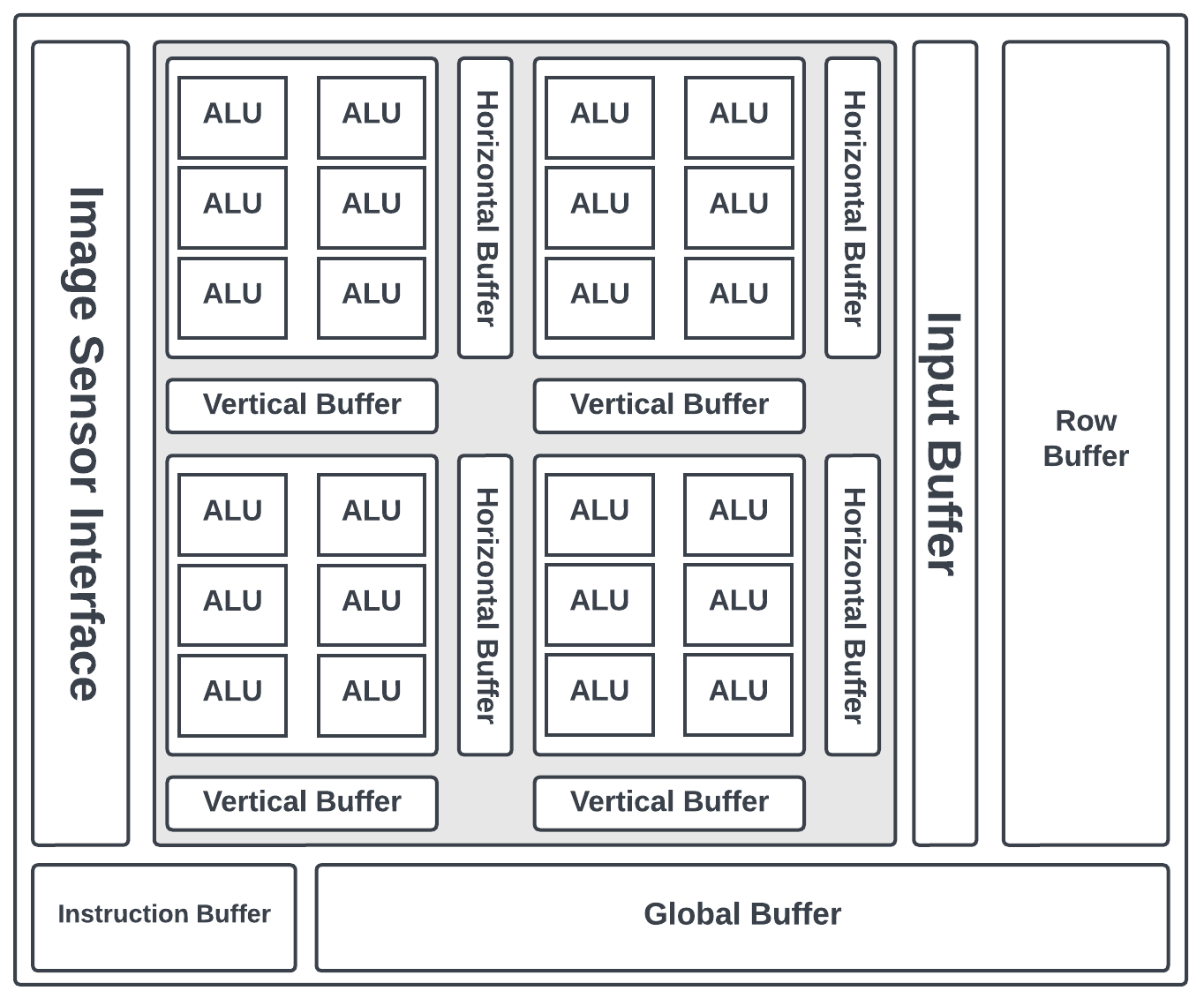
VPUs are a class of ASIC designed to alleviate the heavy processing load on the central processor by accelerating workload-specific tasks. VPUs shown in Fig. 2.10 have a distinct hardware design that focuses on accelerating specific types of computations, such as deep learning inference, video encoding/decoding, and image processing. They often incorporate dedicated execution units, tensor cores, or specialised instructions to accelerate these tasks efficiently.

VPUs employ hardware architectures and software frameworks tailored to exploit parallelism and optimise performance for these tasks. GPUs, while also capable of accelerating AI workloads, are designed to handle a wide range of general-purpose graphics and compute tasks, making them more versatile but potentially less optimised for specific workloads.

VPUs also prioritise energy efficiency, aiming to deliver better performance per watt over other accelerators. They employ techniques like low-power execution units, reduced precision compute, and power management features to minimise energy consumption. GPUs, on the other hand, focus more on delivering absolute performance, often consuming more power in exchange for higher computational capabilities. In addition, VPUs often have specialised APIs or libraries that target specific applications or frameworks, enabling efficient execution of AI models or video codecs. However, the programming ecosystem for VPUs is limited in comparison to general-purpose architectures.

Neural Processing Units (NPUs)

NPUs initially emerged in embedded devices as efficient AI inference accelerators specifically designed to manage the computational demands of machine learning workloads. The initial NPU architecture integrated high-density MAC arrays such as 2D GEMM or 3D systolic arrays since the majority of the computations are found within convolutional layers, which involve significant matrix multiplications. As CNNs continued to become increasingly complex with higher depth and many layers configurations, NPU has now optimised the MAC array structures to ensure enhanced modularity and scalability. Furthermore, newer features such as:

Fused operations

Sparsity acceleration

Unified High Bandwidth Memory

Multi-level array partitioning

Mixed Precision Support

NPUs have expanded their capabilities for other neural network architectures. This includes RNN/LSTM structures, targeting for audio and natural language processing, and transformers.

Neuromorphic Hardware

Neuromorphic architectures are a type of hardware developed to mimic the structure and function of the human brain’s neural networks. These architectures aim to replicate the principles of neural function in their operation, seeking inspiration from biological systems. By incorporating concepts such as weighted connections, activation thresholds, short and long-term potentiation, and inhibition, neuromorphic architectures aim to perform distributed computation in a way that resembles how the human brain processes information.

The key objective of neuromorphic architectures is to achieve efficient and parallel processing of data by leveraging the inherent capabilities of neural networks. These architectures often involve the use of spiking neural networks, where information is transmitted through spikes or pulses, similar to how neurons communicate in the brain. This approach allows for event-driven and energy-efficient computation, making neuromorphic architectures suitable for various tasks, including sensory data processing, pattern recognition, and complex decision-making. Despite their promising advantages, they face challenges, including complexity in design and implementation, limited applicability to specific tasks, scalability issues, lack of standardisation, and difficulty in implementing learning and adaptation mechanisms. Balancing energy efficiency and performance is another challenge, and commercial availability remains limited.

ASIC Summary

Table [tab:ASIC_specs] offers a concise overview of various ASICS. These ASICs serve diverse purposes, from machine learning acceleration to edge computing and AI inference. Notable entries include the Intel Movidius Myriad X, known for its use in edge devices, and the Google TPU, a powerful tensor processing unit designed for machine learning tasks. The ARM Ethos-U55 and Huawei Kirin ASICs are optimised for IoT devices and smartphones, all while operating at low power consumption. Graphcore’s IPU, on the other hand, stands out with its high power requirements, tailored for AI workloads in data centres. Lastly, the Intel Neural Compute Stick focuses on applications such as machine translation and natural language processing.

Heterogeneous Architectures

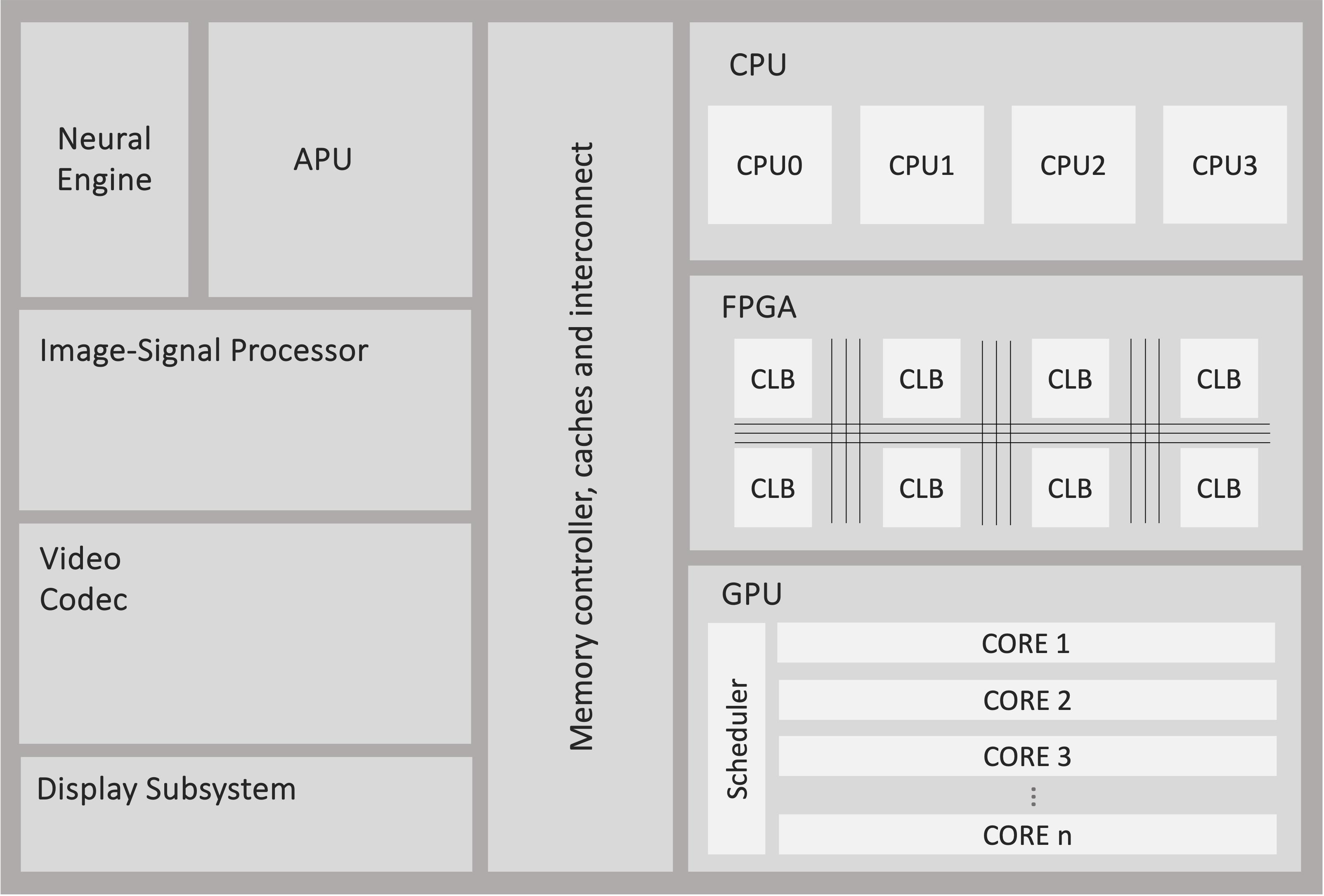
Heterogeneous architectures have recently gained significant attention and mainstream appeal in various application domains. These architectures integrate different types of accelerators, including CPUs, GPUs, NPUs, and FPGAs, into a single compute fabric, observed in Fig. 2.11. Currently, commercial heterogeneous chips only contain a combination of CPU-GPU-NPU[19]. The primary objective of heterogeneous architectures is to accelerate complex tasks by allocating specific operations to the most suitable specialised cores that can process them efficiently.

One of the key challenges in utilising heterogeneous systems lies in algorithm design. Designing algorithms that can effectively leverage the capabilities of different accelerators is crucial. It requires careful consideration of the characteristics and strengths of each accelerator, as well as the partitioning and mapping of computational tasks to the appropriate cores. Algorithm designers need to analyse the computational requirements, data dependencies, and parallelism inherent in the application to optimise the workload distribution across different cores.

Partitioning and mapping refer to the process of breaking down the computational tasks and mapping them onto the available cores. It involves considering the data dependencies, communication overhead, and resource utilisation to ensure efficient execution. Additionally, scheduling tasks across different cores, managing synchronisation between them, and optimising interconnect requirements are critical aspects of achieving optimal performance in heterogeneous architectures.

The programming environment for heterogeneous architectures can be complex and diverse. Each accelerator may have its own programming model, APIs, and language extensions, making it challenging to develop applications that can fully exploit the capabilities of all accelerators. Furthermore, the availability of libraries and software tools may vary across different compute elements due to differences in instruction set architectures. This can lead to binary incompatibility and limit the portability of applications across different accelerators. Evaluating the performance of heterogeneous architectures requires comprehensive performance evaluation techniques. Benchmarks and performance metrics need to consider the characteristics of the application, workload distribution, and communication patterns to provide an accurate assessment of the system’s capabilities.

Summary

The table [tab:HardwareSummary] provides a concise overview of various hardware architectures used in compute operations. CPUs and GPUs offer general-purpose flexibility, supporting temporal and spatial computations with medium and high latency, respectively, while following an instruction-based execution paradigm. FPGAs, though generally flexible, are better suited for spatial computations, with limited practicality for temporal tasks due to overhead and effectiveness constraints. They employ a dataflow execution paradigm. In contrast, ASICs are fixed-function hardware designed for specific spatial computations, offering low latency and following a dataflow execution paradigm.

Software Ecosystem

This section explores the software domain employed for targeting hardware architectures and software interfaces. Optimised libraries such as OpenCV, High-Level Synthesis, and Domain-Specific Languages assume a role in bridging the gap between hardware and software application development.

High-Level Synthesis (HLS)

High-level synthesis (HLS) is a tool that enables hardware designers to use a high-level programming language, such as Python, C or C++, to create hardware designs. This is in contrast to traditional hardware design methods, which involve manually writing hardware description languages (HDLs) such as VHDL or Verilog. HLS tools take in the high-level source code and automatically generate the corresponding HDL code. This can greatly simplify the design process, making it more accessible to non-hardware design experts. This means that designers can focus on the functionality of the design and not worry about low-level implementation details. HLS tools also perform optimisation to improve the performance and resource utilisation of the generated hardware. This can result in more efficient designs that use fewer resources and run faster.

Another benefit of HLS is that it allows for faster design iteration. As the design can be expressed in a high-level programming language, it can be easily modified and re-synthesised to see the effects of the changes. This can greatly speed up the design process and allow for faster time-to-market. In addition, FPGAs are often selected for systems where time to market is critical in order to avoid lengthy chip design and manufacturing cycles. The designer may accept the increased performance, power, or cost in order to reduce design time. Modern HLS tools put this trade-off into the hands of the designer; with more effort, the quality of the result is comparable to handwritten RTL (register transfer language). ASICs have high manufacturing costs, so there is a lot of pressure for designers to achieve success on the first attempt. Design iterations can quickly and inexpensively be done without huge manufacturing costs.

However, these tools come with a set of drawbacks. For instance, the initial learning curve can be steep, particularly for those new to hardware design, as they require a solid understanding of both high-level programming and hardware optimisation techniques. While HLS tools automate the allocation of hardware resources based on the provided code, they may not always yield the most efficient designs for complex projects compared to manual, fine-tuned hardware descriptions. One of the key challenges in using HLS tools is accurately predicting the performance of the generated hardware. Factors such as memory access patterns, data dependencies, and the overall architecture can significantly impact performance, making it challenging to estimate how the synthesised hardware will behave. Moreover, debugging HLS-generated designs can be complex. Traditional software debugging methods are often insufficient, as hardware-related issues might not manifest in the same way as in software. This can prolong development cycles and hinder the identification of issues.

Domain-Specific Languages (DSL)

Domain-specific languages (DSLs) are programming languages designed to address specific problem domains rather than being general-purpose languages. DSLs offer higher-level abstractions and syntax tailored to a particular application area, allowing users to express domain-specific concepts more concisely and intuitively. Unlike general-purpose languages, DSLs enable non-experts to work effectively within a specific domain, as they are more focused on the domain’s requirements and semantics. DSLs come in two main types: external DSLs, which are standalone languages distinct from the host language (e.g., Cal Actor Language[20]), and internal DSLs, which are embedded within a general-purpose language using its syntax and tools (e.g., Halide [21]). The use of DSLs can lead to improved productivity, reduced error rates, and better code maintainability in specific application areas.

Libraries & Frameworks

Optimised libraries such as OpenCV[22] are essential tools used to develop vision and deep-learning applications. These libraries offer a comprehensive collection of pre-built algorithms and functions for a wide range of image-related tasks. Their significance lies in the substantial time and resource savings they provide, enabling developers to utilise tried-and-tested algorithms, thus reducing development efforts and benefiting from community-driven improvements. Moreover, optimised libraries ensure cross platform compatibility, supporting various programming languages and platforms. They are continually updated to harness advancements in hardware and software, making them key for efficient and adaptable image processing.

Deep learning frameworks such as Pytorch[23] offer abstraction and simplification, allowing developers to focus on high-level tasks. Frameworks encompass a comprehensive suite of support programs, compilers, code librar-ies, toolsets, and application programming interfaces that provide a cohesive environment that streamlines the development of systems. Therefore, frameworks facilitate rapid prototyping and integration with other tools.

Conclusion

In conclusion, this section provides an in-depth overview of the imaging pipe-line and its fundamental components, establishing the groundwork for the subsequent chapters. It encompasses typical operations present in each pipeline stage, which will used as implementation examples. Furthermore, the section delves into diverse hardware platforms such as CPUs, GPUs, VPUs, and FPGAs, each offering distinct attributes that can accelerate algorithms. To leverage these hardware capabilities, a range of tools and methodologies are introduced, which include high-level synthesis. In the next chapter, the state-of-the-art study on heterogeneous architectures and optimisation strategies related to image processing are discussed.

State-of-the-Art

This chapter surveys the literature relevant to the research conducted in this thesis. The work covered in this section spans a wide range of topics, including image processing, CNNs, hardware, algorithmic, and domain-specific optimisation approaches. Additionally, the chapter reviews proposed heterogeneous platforms and partitioning methods. A critical analysis of recent research publications is performed, and potential areas for exploration are discussed throughout the section.

Hardware Targeting Image Processing

This section introduces imaging algorithms implemented on various architecture configurations found within the literature. Heterogeneous architectures, which integrate diverse computing elements like CPUs, GPUs, FPGAs, and specialised accelerators, have emerged as a pivotal paradigm in modern computing systems, aiming to achieve higher performance and energy efficiency. These architectures cater to the diverse computational needs such as parallelisation or pipelining for tasks involving deep learning to signal processing. In addition to the literature on supporting algorithms that are tailored to exploit the unique capabilities of these heterogeneous components. Furthermore, various optimisation methods are explored for each hardware.

Multi-Core CPU Architectures

While accelerators with numerous cores such as GPUS, have traditionally outperformed CPUs in image processing due to core count, the recent introduction of many-core CPUs boasting thousands of cores has become more competitive in runtime performance. Furthermore, considering the initialisation and memory latency required for GPUs, CPUs may complete kernels within that timeframe [24], [25], [26].

Many-core co-processors, relying on simple hardware, place substantial demands on software programmers, while their use of in-order cores struggles to tolerate long memory latencies. In addressing these challenges, work has been done to explore decoupled access/execute (DAE) mechanisms for tensor processing. One software-based method is to use naïve and systolic DAE, complemented by a lightweight hardware access accelerator to enhance area-normalised throughput. This method has shown \(2-6\times\) performance improvement on a 2000-core CPU heterogeneous system compared to an 18-core out-of-order CPU baseline[27]. Executing fundamental image processing operations, such as Winograd-based convolution, on many-core CPUs (Intel Xeon Phi), has shown comparable performance for 2D ConvNets. Additionally, it has demonstrated \(3\times-8\times\) times better runtime performance for 3D ConvNets compared to the best GPU implementations[28].

CPU-GPU Architectures

The CPU-GPU architecture is a widely adopted approach to implementing of complex image processing algorithms. The architecture leverages many simple processing cores, which are efficient in executing parallelised tasks. The CPU is typically responsible for orchestrating the high-level control flow and task management allocation to the GPU. Many works developing image processing algorithms on GPUs[29], [30], [31] have exhibited a \(10\sim20\)x speedup in runtime compared to single CPU implementations. In real-time imaging, works such as optical flow[32] and edge-corner detection[33] were evaluated for their algorithmic performance on GPUs and FPGAs. The results observed show that GPUs slightly outperform FPGAs by utilising large amounts of data parallelism and hiding latency. Dynamic thread scheduling on the GPU hides memory latency by swapping threads and making memory requests with others, as long as there are enough threads to keep the process continuous. In addition, easy programmability of GPUs supports software debug iterations which involve fast edit/compile/execute cycles compared to the much more time consuming FPGA[34].

CPU-FPGA Architectures

FPGA:

FPGAs have been utilised for image processing in order to leverage their unique architectural characteristics, such as parallelism, reconfigurability, and low latency. These features enable FPGAs to excel in tasks that demand real-time analysis of image data and require lower power consumption[35].

One major drawback of using FPGAs for image processing is the need to primarily use fixed-point arithmetic. While FPGAs can handle floating-point arithmetic, it often demands too many resources, especially for parallel processing. Vision research typically relies on floating-point algorithms, and adapting them to fixed-point requires a detailed analysis to determine necessary precision at each stage and to work within the FPGA’s resource limits[36]. When compared directly to ASIC devices, disregarding cost and design timelines, FPGA implementations are generally less efficient due to the configuration circuitry overhead, which includes I/O and the required SRAM cells to store the current design. This results in larger device sizes and higher power consumption. ASIC design processes also enable circuitry optimisation for faster clock speeds than those achievable on FPGAs[37].

CPU-FPGA:

Historically, these two components operated independently, each catering to its own application domains. However, in recent years, manufacturers have recognised the complementary strengths of CPUs and FPGAs. This has led to the development of integrated systems, which can be split into two categories, which are soft or hard processors. A soft processor is realised using the programmable logic resources of an FPGA. It’s essentially a processor described in a hardware description language, such as VHDL or Verilog, which is then synthesised and mapped onto the FPGA’s logic blocks. This design offers flexibility, allowing designers to modify the architecture, add custom instructions, or adjust interfaces as needed, with Xilinx MicroBlaze[38] and Intel Nios V[39] being notable examples. In contrast, a hard processor is a physical processor core embedded directly into the FPGA silicon which is optimised and hard-wired for better performance and efficiency. The ARM Cortex cores found in newer Xilinx’s Zynq FPGAs[40] are typically connected to the programmable logic elements through an AXI (Advanced eXtensible Interface) protocol for efficient data transfer and communication.

Initially, soft CPUs were utilised for pre-processing, task scheduling, and resource management. However, collaborative execution, where tasks are computed by both accelerators, have emerged as a prominent approach for increasing application performance, as demonstrated in the literature [41], [42], [43]. In image processing, soft processors have been shown to be more energy efficient and have comparable runtimes than their counterpart discrete processors for low-high complexity algorithms, which is shown in the works [44], [45], [46]. The performance gains extend into the deep learning domain such as CNNs are presented in literature [47], [48], [49], [50].

In summary, hard processors typically outperform soft processors in both speed and resource utilisation due to their independence from FPGA fabric speed and separate chip placement, resulting in enhanced clock speeds and efficient data path designs. Soft processors excel in power efficiency and adaptability, catering to scenarios prioritising energy-conscious designs and dynamic modifications during rapid prototyping and development stages. The architectural distinctions align each processor type with specific application requirements within FPGA-based computing landscapes.

CPU-GPU-FPGA Architectures

FPGAs offer the advantage of direct hardware mapping for efficient implementation of CNNs[51], but they are often constrained by limited on-chip resources[52]. The complexity and size of state-of-the-art CNNs often exceed the available logic and memory resources on a single FPGA chip. To mitigate this limitation, a heterogeneous approach can be employed where different layers of the CNN are mapped onto both FPGA and GPU platforms. This leverages the FPGA’s efficiency for specific layers while utilising the GPU’s computational power for more complex layers, thereby creating a balanced and optimised system.

Recent work into partitioning and executing algorithms onto heterogeneous CPU-GPU-FPGA architectures has been explored in the literature, collected in Table [CPUGPUFPGA]. The platforms category records the combination of accelerators that compose the heterogeneous platform in which the algorithm has been distributed across. The results for energy gain and runtime speedups are derived from comparing the algorithm executed on a single GPU. Partitioning strategy refers to the level of detail at which operations are divided on a heterogeneous platform. In a coarse-grained implementation, entire algorithms or large functional blocks are distributed across different processors within the system. Conversely, a fine-grained implementation maps individual components or layers of an algorithm to specific processors, allowing for more targeted optimisation and resource utilisation. Across all studies, a range of \(1\sim4\times\) speedup and \(1\sim2.3\times\) energy improvement is observed from various partitioning techniques. The key areas identified from all works are that the limiting factors for performance are communication latency, resource availability, coarse partitioning strategies and limited optimisations. In all works, CNN algorithms were implemented partially (e.g., Convolution Layer Only) or did not pass data to other accelerators, therefore not utilising true heterogeneity.

ASIC Architecture

ASICs are highly efficient because they are purpose-built and don’t require additional support hardware. They integrate all necessary components on a single chip, minimising external dependencies and reducing overall system complexity, making them ideal for streamlined and dedicated image processing tasks[53], [54]. VPUs have been shown to achieve similar performance to reference CPUs, GPUs and FPGAs. Additionally, benchmarking of NPUs within mobile platforms has shown to be better in runtime than desktop CPUs and comparable to GPUs while consuming less energy[55].

Image Processing Optimisations

Optimisations are necessary for improving overall system performance, There are three primary categories. First, Hardware optimisations which include optimising memory architectures, computation engine and integrating additional accelerators. Algorithmic optimisations focus on improving the computational procedures, ensuring efficient solving strategies. Lastly, domain-specific optimisations leverage domain knowledge and characteristics inherent to image processing which aim to improve performance, accuracy, and computational efficiency. This section explores optimisation techniques tailored for image processing and CNN algorithms across various hardware accelerators, primarily focused on FPGAs.

Hardware Optimisations

In image processing, memory usage primarily contributes to overall energy consumption and runtime, especially when algorithms require complete frames to be stored in memory[56]. However, accelerators such as FPGAs have resource limitations, making efficient utilisation critical for meeting performance, size, and power constraints[57]. Hardware-based memory optimisations can be classified into on-chip and off-chip categories:

On-chip: Involves optimising the use of fast but limited on-chip memory resources like Block RAM in FPGAs or L1/L2 caches in CPUs and GPUs.

Off-chip: focuses on optimising the use of larger but slower off-chip memory like DDR RAM.

Line buffers are a memory optimisation technique used in convolution-based algorithms by minimising redundant memory access. The first few lines of the image or signal are loaded into the line buffer, marking the only time these lines are fetched from the main memory. As the convolution operation progresses through the image or signal, the lines already in the buffer are reused to calculate multiple output pixels, thereby eliminating the need to fetch the same lines from the main memory again. When moving to the next set of lines, the buffer shifts, discarding the oldest line and fetching a new one to ensure that the lines immediately needed for the convolution are always available. This data reuse and line shifting minimises the number of times the slower main memory has to be accessed. Line buffers have been explored throughout literature [58], [59], [60], [61]. Ping-pong buffers employ a dual-buffering scheme, where two or more buffers alternate roles in a synchronised manner. This approach allows one buffer to be filled with new data while the other is being processed, thereby increasing the throughput by speeding up the read/write process [62], [63], [64].

Pipelining is a technique used to increase the throughput by partitioning complex operations into discrete, independent stages implemented within logic elements like LUTs and flip-flops. Each stage performs a specific operation and is clocked separately, allowing for concurrent execution of multiple data elements across stages shown in Fig. 3.2. In the works of, Jiang et al.[62] and Bai et al.[63], significantly improved throughput in their designs, the data generated by each operation was transferred to the next operation without storage, reducing resource consumption and off-chip latency. Additionally, It is important to ensure stage independence for maximum parallelism and to balance resource utilisation to avoid bottlenecks.

Look-up tables (LUTs) are an effective optimisation technique to increase efficiency[65], [66]. LUTs pre-compute and store the results of frequently used operations, allowing for rapid retrieval and eliminating the need for redundant calculations. In addition, for more complex expressions, such as square roots or multiplying and dividing by an arbitrary number, look-up tables (LUT) and raster based incremental methods can offer improved performance.

Memory architecture can significantly impact both performance and energy efficiency, especially when dividing on-chip memory into smaller blocks to allow parallel access and reduce latency. However, the choice of parallelism influences the required memory organisation and, consequently, the total energy consumption, which is explored in literature[67], [68]. Following on previous works, Tessier et al.[69] showed on-chip power reduction through converting user-defined memory specifications to on-chip FPGA memory block resources. FPGAs often have fixed-size memory that may not align well with the task at hand, leading to energy overhead. Partitioning techniques are therefore required to efficiently manage the storage and processing needs of image data. In the work, Garcia et al.[70], showed that effectively partitioning image frames into BRAMs in order to maximise utilisation (ie, minimise the number of required on-chip memories) can reduce power consumption without affecting the performance. Various off-chip caching systems have been developed to mitigate the latency overheads, such as a three-level memory access architecture proposed by Zhang et al.[71]. This architecture includes off-chip memory, on-chip buffers, and local memories. Nonetheless, the system entails significant waiting times for valid signals between Block RAMs (BRAMs) and off-chip memory, introducing delays.

Approximate computing techniques can significantly improve computational throughput and energy efficiency in image processing tasks when implemented on FPGAs[72]. These methods trade off a small degree of accuracy for performance gains. Two primary strategies are generally used: the first leverages approximate arithmetic for reduced-precision calculations, while the second aims to decrease the total number of operations without substantially affecting output quality. These approaches can be integrated into the learning or optimisation stages to balance both accuracy and computational demands effectively. One study has shown using lower-bit precision like INT8 and INT4 significantly speeds up neural network inference on various architectures. For example, INT8 inference led to up to 5.02× speedup on GPUs, and INT4 added another 50-60% speed gain. Mix-precision further improved ResNet50’s speed by 2% without accuracy loss. These benefits extend to non-GPU platforms, achieving up to 2.35× speedup [73].

CNN Hardware Optimisations

CNNs have now become a popular method of feature extraction and classification. Therefore, this section explores hardware-based optimisation techniques that improve performance. Optimising CNNs on hardware accelerators requires careful algorithm-to-hardware mapping and resource management. The convolutional and fully connected layers are typically the most resource-intensive in terms of both computational logic and memory footprint. Specifically, the storage of high-precision weights and biases for these layers can consume substantial portions of on-chip memory, while the multiply accumulate (MAC) operations required for convolutions and activation’s demand significant computational resources as discussed by Laith et al.[74].

Multiple techniques address these challenges. Firstly, pruning is a compression technique that reduces the model’s complexity[75]. These methods identify and remove weights and neurons that contribute minimally to the model’s predictive performance, usually based on certain statistical or empirical thresholds. Pruning lessens the memory footprint, reducing the storage required for high-precision weights and biases. At its simplest level, pruning removes the smallest weights, setting them to zero as demonstrated by Song et al.[76]. When optimised for energy consumption, pruning techniques that target the least energy-consuming weights achieved a \(1.74\times\) gain in efficiency compared to traditional approaches [77]. In both methods, the pruned network is fine-tuned to maintain the classification accuracy. Multiple studies demonstrate that pruning eliminates \(53\%\) to \(85\%\) of weights in a CNNs convolutional and fully connected layers while losing around \(0.5\sim1\%\) accuracy [78], [79]. Table [tab:hardware_optimisations] summarises optimisations techniques found in hardware.

Domain-Specific Optimisations

Domain-specific optimisations within the imaging domain are methods tailored to increase the performance of applications. These optimisations leverage the unique characteristics of image processing. Such optimisations often involve exploiting properties like spatial locality, symmetry, and redundancy present in images. In literature, there has been very little research on platform agnostic domain-specific optimisations of imaging algorithms on FPGAs. Domain-specific tools and optimisations, particularly in areas such as compilers [80], [81], [82], have been explored but not yet reached maturity.

In the field of image processing, domain-specific optimisations aim to significantly reduce computational load while maintaining consistent accuracy. Examples of such optimisations include down-sampling [83], approximation[84], data-type conversion [85], kernel size adjustments [86], bit-width modification [87], and the complete removal of certain operations. Although hardware acceleration techniques for algorithms on CPUs, GPUs, and FPGAs have been extensively researched [88], [89], [90], these studies generally focus only on target algorithms. In contrast, there has been limited work on exploring the performance and accuracy trade-offs of domain-specific optimisations of imaging algorithms specifically for FPGAs.

Downsampling is a popular method used to reduce the amount of data in an image by selectively removing samples. This involves reducing the resolution of an image by eliminating pixels, usually through averaging or taking the value of a representative pixel in a local neighbourhood. The aim is to decrease computational complexity and storage requirements, making it easier to process and analyse the data. However, downsampling comes with the trade-off of losing some level of detail, which may be critical for certain applications. It is essential to choose an appropriate downsampling factor and method to balance computational efficiency with the preservation of important features in the data.

Fast Fourier Transform is an algorithm to compute the Discrete Fourier Transform (DFT) and its inverse in a more efficient manner. It capitalises on the properties of symmetry and periodicity in the Fourier domain to reduce the number of arithmetic operations. Instead of directly convolving spatial or time-domain signals, FFT first transforms both the input signal and the kernel into the frequency domain. Here, the convolution operation transforms into a simpler element-wise multiplication. After this multiplication, an inverse FFT (IFFT) is applied to bring the data back to the spatial or time domain. The FFT algorithm reduces the computational complexity from \(O(n^2)\) for direct convolution to \(O(n \log n)\), making it highly efficient, especially for larger kernels. The use of FFTs in image processing is found in many works [91], [92], [93]. However, FFT is hardware-intensive due to its high memory bandwidth requirements and arithmetic complexity, which can lead to increased power consumption.

Additional work by Qiao et al. [94] proposed a minimum cut technique to search fusible kernels recursively to improve data locality. Rawat et al. [95] proposed multiple tiling strategies that improved shared memory and register resources. However, such papers propose constrained domain-specific optimisation strategies that exclusively target CPU and GPU hardware. In related work, Reiche et al. [96] proposed domain knowledge to optimise image processing accelerators using high-level abstraction tools such as domain-specific languages (DSL) and reusable IP-cores. Additional optimisation techniques commonly used in general-purpose computing, such as loop unrolling, fission, and fusion, do not map effectively onto FPGA architectures due to the distinct operational paradigms and resource constraints inherent to FPGA design. Consequently, there is a need for the development of accelerator-agnostic and domain-specific optimisation strategies that can be universally applied across diverse computational platforms, including CPUs, GPUs, and FPGAs, for a more cohesive and efficient heterogeneous design.

Algorithmic Optimisations

Algorithmic optimisations refer to techniques employed to exploit mathematical properties or patterns in the data being processed. Strategies may include the use of more efficient data structures, dynamic programming, divide and conquer techniques, and algorithmic transformations. Convolution operations are used in many image processing algorithms which typically account for the majority of computation time. Various algorithmic convolution optimisation strategies are discussed below:

The Strassen[97] algorithm optimises matrix multiplication through recursive partitioning. Given two \(n \times n\) matrices, \(A\) and \(B\), it divides each into four submatrices and recursively computes seven intermediate products (\(M_1\) to \(M_7\)). These products are combined to yield the final matrix using additions and subtractions. The algorithm’s time complexity of \(O(n^{\log_2{7}})\) improves upon the \(O(n^3)\) complexity of naive multiplication, particularly advantageous for larger matrices. However, its practicality diminishes for smaller matrices due to increased constant factors and memory requirements associated with additional operations. The algorithm has shown to be effective in reducing the computational complexity without losing accuracy in CNN algorithms[98].

The Winograd[99] filter algorithm utilises minimal filtering algorithms to perform convolutions, particularly advantageous for small kernel sizes \(K \leq 3\). It transforms the convolution operation into a set of polynomial multiplications in a transformed domain. The idea is to decompose the convolution into smaller, overlapping tiles and then apply the Winograd transformation to each tile separately. This results in a significant reduction in the number of multiplicative operations, which are computationally more expensive than additive operations. Numerous works in literature implementing and comparing Winograd performance [100], [101]. In comparison to FFT-based methods which also reduce the number of multiplications by transforming the convolution into a point-wise multiplication in the frequency domain. However, these methods introduce the overhead of complex-to-real transformations and are more computationally intensive for small kernel sizes due to the increased number of additions and the need for padding.

Specific image processing algorithms often require sorting pixels (e.g., median filtering). These algorithms can benefit from parallel sorting network algorithm optimisations. Sorting networks consist of a predefined sequence of compare-and-swap operations, often organised in a pipeline or tree-like structure, enabling simultaneous execution. In the case of median filtering, sorting networks such as Batcher’s Odd-Even Mergesort[102] can be implemented to sort the values in the input window in parallel, thereby reducing time complexity[103].

In CNNs, algorithmic optimisations are commonly used to reduce runtime for both convolutional and fully connected (FC) layers. General Matrix Multiply (GEMM) is a key method for implementing these layers, as indicated in [104], [105]. In the FC layer, GEMM proves effective for batch processing feature maps (FMs), organised as a \(CHW \times B\) matrix. In which \(C\) represents the number of channels, \(H\) for height, \(W\) for width, and \(B\) for the batch size. This approach optimises computational throughput and memory bandwidth by loading weights just once per batch. Given that FC layers house the majority of CNN weights, GEMM significantly enhances computational speed, especially with increasing sparsity in the FC weight matrix.

High-Level Synthesis

High-level synthesis (HLS) is a potential solution to increase the productivity of real-time image processing development on FPGAs. In order to close the performance gap between the manual and HLS-based FPGA designs, various code optimisations that exploit FPGA architecture for potential speedups are made available in today’s HLS tools. At present, there are various high-level synthesis compilers that are being developed commercially and in academia, shown in table [tab:HLS].

Efficient code optimisation by HLS compilers is vital in real-time image processing applications, where the goal is to minimise execution time and resource utilisation [106]. Furthermore, the quality of generated Register Transfer Level (RTL) descriptions in High-Level Synthesis (HLS) is found to be influenced by the high-level language used, prompting a need for optimised approaches [107]. Notably, comparative research underscores significant performance gaps between HLS-based designs and manually crafted counterparts for intricate applications [108], [109], [110]. Noteworthy disparities of up to 40 times in performance have been documented, particularly evident in demanding tasks like high-definition stereo matching.

Several contemporary avenues in HLS compiler optimisation merit exploration. In the work [111], investigates the impact of compiler optimisations on hardware generated by HLS tools, highlighting the significance of both the optimisation strategies and their sequential application order in enhancing the RTL output quality. In addition, a subsequent study [112], refines the understanding of HLS-based real-time image processing design optimisations. Applying a sequence of optimisation techniques, this approach showcases comparable performance when benchmarked against alternative methodologies and industry-standard HLS tools. The optimisations applied in both works include:

Function In-lining: Incorporating functions directly into the code to eliminate function call overhead and improve overall performance.

Loop Manipulation: Adjusting loop structures to enhance computational efficiency and reduce processing time.

Symbolic Expression Manipulation: Utilising symbolic expressions to manipulate mathematical representations for improved computational speed and precision.

Loop Unrolling: Expanding loops by replicating their bodies to reduce loop-control overhead and maximise parallelism.

Array Transformation: Applying various techniques to optimise arrays, the two commonly applied techniques are listed:

Array Partitioning: Dividing arrays into smaller, more manageable partitions to enhance data locality and optimise parallel processing.

Array Reshaping: Modifying the shape of arrays to better align with computation requirements, improving overall efficiency in data processing.

The advantages of HLS tools observed by Wakabayashi et al.[113], on elevating abstraction levels highlight how expressing designs in higher-level languages like C and C++ can significantly reduce code complexity, making them better at managing complex designs more effectively.

Domain-Specific Languages (DSL)

A domain-specific language (DSL) is a specialised programming language for a particular domain, such as image processing. The following paragraphs look into some recent developments of DSLs within image processing. In contrast to C/C++ with HLS tools, DSLs provide clearer syntax, rigorous semantic checks and possible compiler domain optimisations for improved generated code. A summary of available DSLs is found in Table [tab:DSL].

Richard, Membarth et al.[114] proposed a new DSL and source-to-source compiler for image processing called ’Hipacc’. They show that domain knowledge can be captured to generate tailored implementations for C-based HLS from a common high-level DSL description targeting FPGAs and GPUs. The image processing algorithms that were generated in VHDL/Verilog code from the DSL are evaluated by comparing them with hand-written register transfer level (RTL) implementations. The results show that the HLS still has deficiencies in contrast to the RTL but enables rapid design space exploration. The Hipacc framework does not generate the hardware descriptor language but relies on Xilinx’s HLS tools for generated HDL optimisations.

In the work by Jocelyn, Serot et al.[115] presented CAPH, a DSL suited to implementing stream-processing based applications on FPGA. CAPH relies upon the actor/dataflow model of computation and the tool suite also contains a reference interpreter and a compiler producing both SystemC and VHDL code. CAPH was evaluated by implementing a simple real-time motion detection on an FPGA platform. This was done to validate the overall methodology and to identify key issues. The results established three research directions to improve CAPH. The first is assessing the tools on larger and more complex applications and comparing them with hand-crafted RTL in terms of resource usage and runtime. The second research direction is improving the compiler and optimising the generated VHDL code. Third, applying static analysis techniques to actor behaviours to statically estimate the size of FIFO channels.

Another DSL for FPGAs was proposed by Robert, Stewart et al.[116] called RIPL. The aim is to increase throughput by maximising clock frequency and minimising resource usage to fit complex algorithms onto FPGAs. RIPL introduces an algorithmic skeleton to express image processing algorithms which are then exploited to generate deep pipelines of highly parallel and memory-efficient image processing components. The data-flow graph generated is expressed in CAL actor language and is compiled into Verilog. The DSL was used to implement image watermarking and multi-dimensional subband decomposition algorithms.

Benchmarking

Benchmarking is a relatively established concept in computing, serving as a crucial tool to gauge the performance of various systems. Identifying the most suitable hardware platform becomes imperative, especially when aiming for efficiency and performance. Yet, the challenge lies in determining this without investing significant time and understanding into implementations. Thus, benchmarking measures performance and aids in making informed decisions about hardware compatibility for complex algorithms.

Numerous benchmarking studies have been conducted on a variety of accelerators, including FPGA [117], GPU [118], TPU [119], and NPU [120]. These studies assess performance using specific metrics and facilitate comparisons between different hardware platforms [121]. Additionally, recent interest in the industry has begun to develop suites such as MLPerf [122] and DataPerf [123] to establish a standardised ML benchmarking and evaluation to allow comparison of inference/training chips or models.

Early work in heterogeneous benchmarking was the introduction of the Rodinia suite in 2009 [124]. Rodinia comprises applications and kernels that embody the behaviours of the Berkeley dwarfs. These are a taxonomy of 13 computational patterns widely used in various scientific domains. The suite also addresses communication, synchronisation, and power consumption issues. However, Rodinia does not leverage newer features, such as advanced heterogeneous programming constructs, half/mixed precision, tensor computations, and libraries that enhance communication between architectures. Instead, Rodinia focuses on more abstract algorithms rather than micro-benchmarks that target specific components.

Scalable Heterogeneous Computing (SHOC) [125] developed in 2010 as another benchmark suite targeting heterogeneous systems. The suite primarily focused on scientific computing workloads, including common kernels such as matrix multiply, fast Fourier transform, and Stencil computation. The benchmark is divided into two testing methods: The stress tests use computationally demanding kernels to identify OpenCL devices with bad memory, insufficient cooling, or other device component problems. The other tests measure many aspects of system performance on several synthetic kernels as well as common parallel operations and algorithms. SHOC supports various versions of benchmarking, from serial to testing inter-communication between architectures. Every application in the SHOC suite operates within a cohesive framework that allows users to define specific testing parameters, including the desired number of iterations. The framework can also capture intricate metrics, such as floating-point operations per second (FLOPS). The drawback to SHOC is that it focuses on basic parallel algorithms, thus missing the nuance of real-world applications; just like Rodinia, it has not been updated to test modern algorithms and cannot scale to larger problem sizes.

In recent work, Mirovia [126] builds upon both Rodinia and SHOC, designed to leverage the newer evolving architectures. While also representing a diverse set of application domains. This includes a particular focus on deep neural networks. Mirovia aims to characterise modern heterogeneous systems better. The benchmark suite falls short in the range of hardware it can target, being limited to Compute Unified Device Architecture (CUDA) enabled GPU only. Other work focuses on a single domain area; QuTiBench [127] is a multi-tiered framework for neural networks which introduces optimisation strategies such as quantisation, which is essential for specific accelerators such as FPGAs. Only the classification stage of the image-signal processing pipeline is tested within the framework; therefore, determining the full performance scope of a vision system is difficult. Reuther et al. [128] proposed a survey and benchmarked machine learning algorithms on commercial low-power ASICs and a CPU. However, such papers propose benchmarks and frameworks for specific algorithms or target singular architectures, focusing only on execution time performance. In addition, power consumption and memory transfer metrics are often missing in such benchmarks, which is a driving factor for embedded systems with limited energy.

Evaluated Image Processing Algorithms

This section outlines the implementation details on hardware (primarily FPGA) and the rationale behind the selection of various algorithms evaluated in the subsequent chapters. All algorithms were partly chosen due to their popular use in many image processing pipelines and varying complexity. The CPU and GPU image processing implementations of all algorithms are derived from OpenCV [22]. The FPGA implementations have been reviewed in literature to develop widely adopted methods (Algorithmically the same as CPU & GPU for fair comparison), which, at best, are close to the most optimal design.

RGB2Grey, Image Addition, Subtraction: These operations serve as fundamental building blocks in image processing pipelines. Converting images to grayscale simplifies processing tasks, reduces memory usage, and enhances contrast for improved feature detection. Grayscale images directly represent luminance, making them useful for detecting subtle brightness variations. In addition, grey images have widespread compatibility, require less storage space, and can help reduce noise levels, resulting in clearer images for analysis. Image addition can adjust brightness or contrast by adding or subtracting constant values, while subtraction can isolate foreground objects through background subtraction or detect changes in scenes over time.

The FPGA colour conversion module declares parameters for the dimensions of the image (m columns by n rows) and defines registers to store the input colour image in BMP format and the resulting grayscale image. Upon initialisation, the module reads the input colour image data from a BMP file into memory. Then, it iterates over each pixel in the image, extracting the red, green, and blue colour values and calculating their sum. This sum is divided by 3 to obtain the grayscale value, which is stored in a register. The image addition and subtraction module functions by performing pixel-wise arithmetic operations between corresponding pixels in two input images. The modules primarily use registers and combinational logic to perform pixel-wise addition/subtraction of two images.

Resizing: Resizing operations are essential for various image processing applications, including scaling images for different display resolutions or aspect ratios. Many algorithms and CNN architectures require images to be resized to reduce computation complexity.

The imageResize module facilitates the resizing of input image data by adjusting its width and depth based on specified scaling factors. The resizing operation involves updating counters for tracking column, row, and pixel positions within the image. As the module receives valid input data and a ready signal, it increments these counters accordingly. When the counters reach the desired scaling factors for width and depth, the module resets them to zero, effectively resizing the image. The output image data is synchronized with the clock signal and becomes valid only when both the column and row counters are zero, ensuring proper alignment with the resized image dimensions.

Erode, Dilate: Morphological operations like erosion and dilation are commonly used for tasks such as image segmentation and feature extraction. The module erodeDilate operates on grayscale images represented by 8-bit pixel values. A 3x3 buffer array is utilised to store neighbouring pixel values for each input image pixel. Upon initialisation or reset, the buffers and output values are cleared. As new pixel values arrive with each clock cycle, the buffer contents are shifted accordingly.

For erosion, the module computes the logical AND operation of all pixels in the 3x3 neighbourhood, resulting in the minimum pixel value. Conversely, dilation computes the logical OR operation, resulting in the maximum pixel value. These operations are performed on the buffer contents corresponding to the current pixel position. Finally, the resulting eroded or dilated pixel value is output along with its validity signal.

Box Filter, Gaussian Filter: Filters like the box filter and Gaussian filter are fundamental for image smoothing and noise reduction.

The Verilog code comprises modules designed for linear filters. The "line Buffer" module functions as a storage mechanism for incoming pixel data, organising it into line buffers to facilitate subsequent convolution operations. It efficiently manages the storage and shifting of pixel data as needed. The "imageControl" module orchestrates the flow of pixel data, determining when to initiate reading and writing operations based on the availability of data and signalling when to begin filtering. It tracks the total number of pixels processed to ensure accurate filtering across the image. The "conv" module is responsible for executing the convolution operation itself. It performs element-wise multiplication of pixel values with corresponding kernel coefficients and aggregates the results to generate the convolved pixel output.

Sobel Filter, Median Filter: The Sobel filter is widely used for edge detection, while the median filter is effective for noise removal. The Sobel operator consists of two 3x3 kernels: one for detecting vertical edges and the other for horizontal edges. The module takes nine input pixel values corresponding to the 3x3 neighbourhood surrounding a central pixel. These input pixels are named according to their relative positions: Within the module, two instances of the matrixmul module compute the gradient components along the x-axis (gx) and y-axis (gy) using the Sobel kernels. The result of each multiplication operation is squared to obtain the squared gradient magnitudes in the gxsquared and gysquared wires. These squared magnitudes are then added together to compute the overall squared gradient magnitude in the squaredsum wire. The sqrt module calculates the square root of the squared gradient magnitude.

The median filter module takes in pixel values (pixelin) of image width and operates on a square filtering window of fixed size. Within each processing cycle, the module updates the window with new pixel values, sorts the window values to find the median value, and outputs the median as the filtered pixel value (pixelout). The algorithm maintains internal registers to store the window and the histogram-based sorted window of pixel values. During reset, the internal registers are initialised, and processing flags are reset.

White Balance: White balance adjustment is essential for achieving accurate colour representation in images captured under different lighting conditions.

WhiteBalance module is designed to perform white balance adjustment on an input image by adjusting the red, green, and blue colour channels. It takes in pixel values for the red, green, and blue channels of the image.

The module maintains buffers to accumulate the pixel values for each colour channel (redsum, greensum, bluesum) and a register to count the number of pixels processed (pixelcount). These registers store the accumulated sums and count, respectively. On each clock cycle, the module accumulates the pixel values and updates the count. Then, it calculates the average pixel values for each colour channel by dividing the accumulated sum by the pixel count. Finally, it applies the white balance coefficients to adjust the colour channels accordingly.

Linearization: & Gamma Correction Linearization and gamma correction are essential in image processing, ensuring consistent pixel representation and adjusting brightness and contrast for good visual images, making them ideal for bench-marking.

The Linearization module is designed to linearize the pixel values of an input image, effectively scaling them to a range between 0 and 1. The module takes an 8-bit pixel value as input and outputs the corresponding linearized value. It employs simple arithmetic logic to divide the input pixel value by 255, the maximum value in an 8-bit system, thereby scaling it to the desired range. The linearization process occurs on each clock cycle, ensuring real-time processing of image data.

GammaCorrection module applies gamma correction to an input pixel value using a real gamma value of 2.2. The module operates synchronously with the clock signal and includes a reset input for initialisation. Inside the module, it takes the input pixel value and applies a power function with an integer approximation of the gamma value. The function then converts the gamma-corrected integer value back to the [0, 255] range to ensure compatibility with pixel representations. The module continuously applies the gamma correction function to the input pixel value on each clock cycle. The output pixel value is updated accordingly. The input and output pixel values are stored in registers.

GEMM: GEMM algorithm serves as a base building block for numerous image processing and deep learning operations due to their algorithmic efficiency in performing matrix multiplications. The algorithm is computed in many areas of ML, such as fully-connected layers, recurrent layers such as recurrent neural networks, Long short-term memory or Gated recurrent unit, and convolutional layers. Benchmarking GEMM allows for assessing the computational performance and scalability of hardware architectures across a wide range of image processing and deep learning algorithms. The optimised FPGA GEMM implementations used for evaluation are provided by Xilinx[129] library.

FFT (DFT): Fast Fourier Transform (FFT) are found in various operations in imaging algorithms by enabling efficient frequency domain analysis and manipulation of images for tasks such as filtering, convolution, registration, texture analysis, edge detection, compression, and super-resolution imaging. Xilinx provided FFT IP-block[130] is used in the benchmarking. The module implements the Cooley-Tukey FFT algorithm for computing both forward and inverse DFTs of sample sizes that are powers of 2.

STREAM: Memory bandwidth and latency are important metrics because they directly impact the speed and efficiency of data transfer between the processor and memory. Therefore, when benchmarking image processing algorithms, measuring memory bandwidth and latency provides insights into how efficiently the algorithms utilise memory resources, helping assess their overall performance and scalability. The implementation used for FPGAs are from HPCC FPGA benchmarking suite[131].

Demosaicing: Demosaicing algorithms are essential for reconstructing colour images from Bayer-pattern sensor data which are common filter used in vision systems. The algorithm is a good choice to benchmark since most vision systems use Bayer filter. Xilinx provided de-mosaicing IP-block[132] is used in the benchmarking. The demosaicing algorithm used is a bilinear interpolation, where missing colour values in a Bayer-filtered image are estimated by averaging neighbouring pixel values.

SIFT: Scale-Invariant Feature Transform (SIFT) is a widely used technique for feature extraction in image processing applications. The FPGA implementation is discussed in Section [SIFTHardwareDesc].

CNN (Classification): Convolutional Neural Networks (CNNs) have become significantly popular methods for image classification, object detection/segmentation tasks. Xilinx Deep Learning Processor Unit (DPU) is used to implement both optimised ResNet-18 and MobilnetV2 architectures[133].

Conclusion

This chapter delves into the discussion and evaluation of diverse heterogeneous architecture implementations, tools, and optimisation strategies. The literature review emphasises that specific processing architectures, such as GPUs, FPGAs, and VPUs, exhibit greater efficiency in executing imaging algorithms than CPUs, owing to their architectural properties (e.g., SIMD, DSP Slice) and depending on algorithmic features like parallelisation and data dependencies. Moreover, these architectures to exploit their advantages leads to further performance gains. Various optimisations have also been shown to enhance the efficiency of image processing algorithms, encompassing techniques such as algorithm replacement, hardware (memory management) and pipelining schemes. However, the knowledge gap is evident in the lack of a systematic approach or set of strategies for partitioning imaging algorithms onto the appropriate hardware accelerators in a heterogeneous platform, nor a comprehensive rationale for such decisions. In addition, there are no end-to-end implementations of CNN and feature extraction algorithms utilising CPU-GPU-FPGA architectures. The absence of image-domain-guided optimisations and understanding of trade-offs further complicates achieving optimal performance and efficiency. Hence, within the scope of this thesis, a robust benchmarking framework that guides algorithm partitioning along with domain-specific optimisation strategies on heterogeneous platforms is proposed.

HArBoUR: Heterogeneous Architecture Benchmarking on Unified Resources

This chapter presents a description of HArBoUR, a heterogeneous imaging framework used for guidance and implementation of various image processing algorithms presented in later chapters. In addition, the chapter contains benchmarks and evaluations of micro/macro image processing algorithms commonly found in imaging pipelines of vision systems. The algorithm suitability on a specific accelerator is determined from the analysis of the results.

Introduction

The advances in multi-core processors and accelerators have enabled real-time embedded imaging algorithms to become ubiquitous within many vision application areas such as advanced driver assist systems (ADAS) [134], surveillance[135] and satellites[136]. The growing demand for image processing algorithms on systems with resource and energy constraints requires architectures that perform tasks efficiently. These hardware accelerators come with various architectures ranging from CPUs, GPUs, and FPGAs. Traditionally, embedded imaging designs often involve implementing image processing algorithms on homogeneous architectures, which come with hardware limitations. However, recent developments introduce heterogeneous architectures that combine multiple specialised accelerators on a singular interconnected chip[137]. These novel architectures provide optimum design opportunities for embedded imaging development. However, current developments in targeting heterogeneous platforms are still primitive and require careful consideration of various development languages, tool-sets and performance profiles to fulfil energy and runtime constraints of applications. Furthermore, certain accelerators have pre-written optimised vision libraries, e.g., OpenCV/CUDA (for CPU/ GPU) and xfOpenCV (for FPGAs). However, the design and development of image processing algorithms in a heterogeneous environment is still an arduous task. It requires in-depth knowledge of multiple hardware accelerators, and each differing in performance due to their underlying architectures. Additionally, FPGA designs require knowledge of hardware descriptor languages (HDLs), which have higher learning difficulty despite the existence of recent high-level synthesis tools or domain-specific languages that abstract away from the underlying hardware. This is due to a lack of understanding and the existence of benchmarks for image processing algorithms on different hardware. Therefore, partitioning complex image processing algorithms onto each accelerator remains a difficult task for application designers.

Benchmarking has played an integral part within the computing domain for decades. Since the beginning of computing systems, there has been a persistent need to evaluate and compare the performance of hardware components. Initially, with the early day mainframe computers to the modern era of microprocessors, GPUs, and custom ASICs, benchmarking has provided a standardised measure to gauge the efficiency, speed, and capabilities of hardware devices. Over the years, benchmarking tools and suites have played a pivotal role in driving technological advancements, guiding design decisions, and ensuring that hardware meets the ever-evolving demands of software applications.

To address the emerging demand for high performance vision hardware, there is a need for a suitable benchmarking framework that dissects the imaging/vision algorithms in a disciplined way and benchmarks their performances (both energy and execution time) on all available target hardware (e.g., CPU, GPU and FPGA). To address such a gap, this chapter proposes a new framework providing a systematic way of implementing imaging designs on specialised platforms and perform benchmarks on representative vision algorithms while assessing execution time, memory latency and energy consumption. System designers will use the proposed framework to identify appropriate hardware for the target application and unlock the potential of a true heterogeneous system. The main contributions of this chapter are:

We propose a framework that studies features of image processing algorithms to identify characteristics. These characteristics help partition complex algorithms into the most optimal target accelerators within heterogeneous architectures.

The approach adopts a systemic and multi-layer strategy that offers trade-offs between runtime, energy and accuracy within the imaging sub-domains e.g., CNNs and feature extraction. Specifically, HArBoUR enables support in constructing end to end vision systems while providing expected results and guidance.

Domain knowledge-guided hardware evaluation of computational tasks allows imaging algorithms to be mapped onto hardware platforms more efficiently than a heuristic based approach.

We benchmark representative image processing algorithms on various hardware platforms and measure their energy consumption and execution time performance. The results are evaluated to gain insight into why certain processing accelerators perform better or worse based on the characteristics of the imaging algorithm.

Benchmarking Framework for Image Processing on Hardware

For efficient implementation on heterogeneous platforms, the algorithm design will require partitioning any image processing algorithm according to its suitability for individual components in the pipeline on the target hardware. Therefore, a standard framework is proposed containing a pool of image processing algorithms and their characteristics in accordance with their hardware suitability. We selected a range of low, medium and high-level algorithms from the image processing hierarchical classification domain, providing wider coverage of commonly used operations performed within a vision application pipeline.

Various algorithmic and hardware characteristics that would impact the performance are identified in the heterogeneous benchmark framework, shown in Fig. 4.1. The framework diagram offers a clear overview of the image processing landscape. It maps out the relationship between hardware properties, optimisations, algorithms, metrics and memory access patterns. This concise visual guide aids designers by offering insights into potential bottlenecks, suggesting areas for innovation, and guiding the fine-tuning of algorithms on heterogeneous platforms to achieve peak performance in imaging tasks.

Processing Pipeline & Operation Types:

Image processing algorithms are organised into three primary domains: Pixel, Kernel, and Image. The Pixel domain focuses on operations that manipulate or query individual pixel values. The Kernel domain encompasses algorithms that utilise a small matrix (the kernel) to modify an image. Lastly, the Image domain deals with operations that consider the image as a whole, where global features and patterns are essential for labelling.

Operator Group

This label specifies the name of the algorithm. Algorithms may perform a particular operation (e.g., Image Arithmetic), but depending on the stage within the image computation pipeline, the data type of the pixel is defined differently and may contain additional values for calibration, such as a pedestal. It is necessary to be explicit when defining the algorithm within the framework. These image processing algorithms can further be categorised into groups (Operation Group) depending on the type of operation it performs.

Image Arithmetic & Pre-Processing:

Image arithmetic and pre-processing are foundational steps in image processing pipelines, preparing images for subsequent analysis. These algorithms predominantly execute primitive operations to transform an input format into a desired one. They typically operate on individual pixels using localised data, which minimises task dependencies. While algorithms like multiplication, accumulation, squaring, magnitude determination, and weighting are arithmetically simple, most architectures can compute them with ease. Given their low initialisation and latency requirements, architectures such as CPUs and FPGAs are particularly well-suited for these tasks.

Geometric Transformation & Image Analysis:

Geometric transformations refer to operations that modify the spatial arrangement of pixels in an image. These transformations can be applied for various purposes, such as image registration, scaling, and augmentation. Typically, these algorithms involve convolution and interpolation operations, which can be linear or nonlinear. Additionally, the choice of interpolation method, whether nearest-neighbour, bilinear, or bicubic, can significantly impact both the quality of the transformed image and the computational complexity of the operation. Several operations are sequentially bound; forward mapping directly calculates new pixel locations but can leave gaps in the output. Its counterpart, backward mapping, determines source contributors for each output pixel and often requires interpolation, which can be sequential, especially with higher-order methods. Warping with a displacement map, which dictates pixel movement, can also be sequential if complex algorithms determine displacements. Resampling, essential post-mapping, can become sequential with intricate interpolation. Cumulative transformations, where multiple operations are applied in sequence, and error corrections post-transformation, further introduce sequential elements. For operations with inherent sequentiality, such as certain geometric transformations, traditional CPUs are often the most suitable due to their optimised instruction sets for sequential tasks and complex branching. However, for tasks within geometric transformations that can be parallelised, GPUs, FPGAs, and TPUs can offer significant speedups

Image analysis algorithms label and understand various statistical data about a pixel. These algorithms have many irregular memory access patterns (mean, mode, min/max) and branching conditions that negatively impact the performance of processing accelerators.

Image Filters & Morphology:

Image filter algorithms modify particular spatial frequencies. The image is filtered either in the frequency or in the spatial domain. Image filters are divided into two categories: linear and non-linear. Linear image filters perform the convolution of an image using a pre-computed kernel for efficiency. The data-independent multiply and accumulate operations coupled with sequential data access of linear filters map well onto GPUs and FPGAs. Contrarily, non-linear filters have varied memory access patterns and have higher arithmetic intensity. Additionally, certain algorithms with branching makes it arduous to implement efficiently on a GPU and FPGA, which can exploit parallelism in these operations. Non-linear filters consist of operations where the output pixel value is determined based on some non-linear function of the input pixel values in its neighbourhood. Examples of algorithms include median, adaptive and bilateral filtering.

In morphological operations, an image is processed with a structuring element, which is a small binary or grayscale mask. The structuring element is moved over the entire image, and at each position, a computation is performed based on the values of the image pixels that overlap with the mask. Architectures with cache hierarchies, prevalent in modern CPUs and GPUs, can exploit this pattern for enhanced cache locality, especially when the structuring element’s dimensions are compatible with cache sizes. In row-major order, horizontal traversal optimises memory access, while vertical traversal can introduce inefficiencies due to memory strides. Basic operations like dilation and erosion have regular patterns, but advanced morphological algorithms can cause irregular accesses. These irregularities, often from adaptive structuring or conditional operations, challenge GPU performance through warp divergence. Additionally, these algorithms may require repeated pixel reads, especially with overlapping structuring elements, and in-place operations risk read-write conflicts, which need careful management to prevent race conditions.

Feature Extraction:

Feature extraction algorithms, such as SIFT[138], SURF[139], and Oriented FAST and Rotated BRIEF (ORB)[140], are designed to identify and describe local features in an image. These features are often points or small image patches that are distinct and can be reliably and robustly detected in various scales of the same scene. The pixels extracted from an image are not stored adjacently in memory and require expensive computational reads from non-adjacent memory addresses that will impact the performance of all processing architectures. Algorithms such as ORB examine a circle of pixels around each candidate pixel. While each keypoint detection is independent and can be parallelised, the algorithm involves conditional checks, which can lead to divergent execution paths.

Regarding hardware suitability, CPUs have a layered hierarchy of caches, encompassing L1, L2, and L3. This architecture is good at offsetting the performance implications of non-sequential memory accesses. Therefore, algorithms with random access patterns, akin to the keypoint detection seen in SIFT or ORB, can leverage this hierarchical structure. Nevertheless, despite their proficiency, CPUs will lag in efficiency when confronted with parallel operations stages within the algorithms. GPUs and FPGAs, on the other hand, are geared towards the parallel processing tasks which are found during the convolution and prefix sum stage. GPUs favour coalesced memory access, where adjacent threads reading consecutive memory locations achieve faster, more efficient data retrieval. Consequently, the random accesses, if frequent, can lead to performance dips due to the resulting uncoalesced memory transactions. However, TPUs are purpose-built for tensor operations, forming the basis of deep learning methodologies. Traditional feature extraction may not have direct advantages from TPUs unless they’re integrated into a wider deep learning framework.

Data Primitive:

This characteristic specifies the type of data unit or collection of pixels an algorithm operates on, encompassing attributes like type, size, and representation. Depending on the level of the pipeline, a pixel may refer to an individual or collection of bits of type word, uint8 or uint12. The following are the various data primitives found within image processing:

Bit: Refers to individual bits in the binary representation of the image data, encompassing pixel values, metadata, file headers, and more, contingent on the file format.

Element: Denotes a discrete scalar value, formed of bits, quantifying pixel attributes, like colour intensity or luminance.

Pixel: Is a set of elements symbolising a point in an image, with formats such as RGB, YUV, or Bayer encoding.

Frame: Is a structured pixel collection visualised in 2D or 3D, where the resolution indicates the total pixel count.

Patch: Is a small frame subsection targeted by algorithms like blurring; a \(3\times3\), \(5\times5\) Kernel is a matrix sliding over the image, its values multiplied with corresponding patch pixels, and the results summed for a transformed image.

Block: Pertains to a contiguous pixel group, typically of fixed dimensions like \(8\times8\) or \(16\times16\), serving as the atomic unit for algorithms, such as JPEG compression.

Blob: Is an image region defined by properties like brightness, distinct from surrounding areas.

Tensor: Is a multi-dimensional structure encapsulating complex data; a 2D tensor represents greyscale images, while a 3D tensor handles colour images, considering width, height, and colour channels. In deep learning, tensors provide a concise mathematical representation of the problem.

Tile: Is a unique image portion, often rectangular, acting as a processing or representation unit. Unlike overlapping patches, tiles traditionally denote non-overlapping image regions, ensuring each pixel’s unique tile membership. Tiling affects memory access patterns and storage; for instance, accessing an image row might require data fetching from multiple tiles if stored tile-by-tile.

Understanding data type precision is essential as it impacts accuracy and hardware suitability. Algorithms requiring higher precision will use floating-point datatype, which is better supported by the FP hard blocks within CPU or GPU architectures, while FPGA solutions suit integer-based calculations. Data primitive choice impacts memory, bandwidth, and computational efficiency. Successful imaging pipeline design hinges on aligning data primitive attributes with processing unit capabilities, thereby optimising image processing workflow in terms of accuracy, efficiency, and hardware compatibility. An optimal pipeline balances various primitives for each operation while maintaining high accuracy.

Access Patterns:

Image pixel locality in memory refers to how the spatial arrangement of pixel data impacts the efficiency of image processing tasks. When pixels are stored in memory, their arrangement influences data access efficiency. Locality in memory means nearby pixels in the image are stored adjacently, aiding faster data access. Various access patterns are discussed below:

Sequential Access: Involves accessing pixels one after the other, typically in row-major or column-major order.

Random Access: Retrieves pixels in a non-sequential manner based on algorithmic requirements.

Neighbourhood Access: Relates to the pixels surrounding a specific pixel, often used in operations with kernels or local filters.

Block Access: Deals with a contiguous region of pixels, common in block-based algorithms or compression methods.

Strided Access: Refers to the method where pixels are accessed at regular intervals or ’strides’.

Pyramidal Access: Is associated with multi-resolution representations, such as image pyramids.

Scanline Access: Involves accessing entire rows or columns of pixels simultaneously, often seen in raster operations.

Tile-based Access: Focuses on square or rectangular pixel tiles, crucial in tiled rendering or processing.

Efficient memory access is crucial in real-time imaging due to computer memory hierarchies. Pixels stored close in memory can be loaded into faster cache levels, reducing time spent waiting for data from slower memory. In image processing, operations like convolution require accessing nearby pixels. Locally stored pixels minimise cache misses and improve computational performance. Techniques like tiling, memory padding, and cache-aware algorithms enhance processing efficiency. By aligning pixel data in memory with spatial arrangement and optimising memory hierarchy, image processing algorithms can leverage hardware effectively for faster performance.

Hardware Characteristics & Edge Handling:

It is necessary to understand the capabilities and limitations of each hardware architecture to obtain optimum accuracy, area and speed of imaging algorithms. These depend on particular hardware properties such as bit-width, clock rate, memory location, data type and data dependency. Image processing algorithms perform poorly on memory systems due to memory hierarchy latency bottlenecks and high cache miss rates. Additionally, architectures containing many processing units require careful division of tasks to avoid load imbalance.

Edge handling involves strategies when operations, such as filtering, convolution and morphological transformations, are applied near the boundaries of an image. Since these algorithms often require neighbouring pixel values, challenges arise at the image edges where full neighbourhoods are unavailable. Common edge handling techniques include zero-padding (extending the image with zeros), replication (duplicating the edge values), reflection (mirroring the adjacent pixels), and circular (considering the image as a continuous loop). Different edge handling techniques can lead to non-uniform or non-sequential memory access patterns. In addition, the choice of method can influence the resultant image, especially in terms of artefacts or discontinuities at the boundaries. Proper edge handling is crucial to ensure consistent and artefact-free processing results.

Optimisations & metrics

The optimisation attribute captures accelerator agnostic optimisations for image processing algorithms. The attribute provides a repository of optimisations that helps designers pick and tune algorithms to find the optimal combination within their design space for specific use cases. These optimisations focus on the inherent properties of the algorithm, such as reducing computational complexity, improving data access patterns, or refining logical structures. The primary reasoning is their broad applicability and ensures a performance baseline. The improvements realised are typically consistent across various hardware architectures, from CPUs and GPUs to FPGAs and ASICs.

The metric attribute standardises performance indicators from benchmarking literature, facilitating an understanding of trade-offs. Metrics such as runtime assess algorithmic execution speed, throughput quantifies data processed over time, and energy per operation provides insights into energy efficiency. For neural networks, accuracy measures how often the model is correct, precision looks at how many of the positive identifications were actually right, and the F1 score balances precision against recall.

Heterogeneous Benchmarking Development Flow

Heterogeneous hardware addresses the growing complexity of modern workloads by combining different processing units, such as CPUs, GPUs, and other accelerators, within a single system. This approach optimises performance and energy efficiency for specific tasks, leveraging the strengths of each component. However, targeting these platforms remains a significant challenge to address.

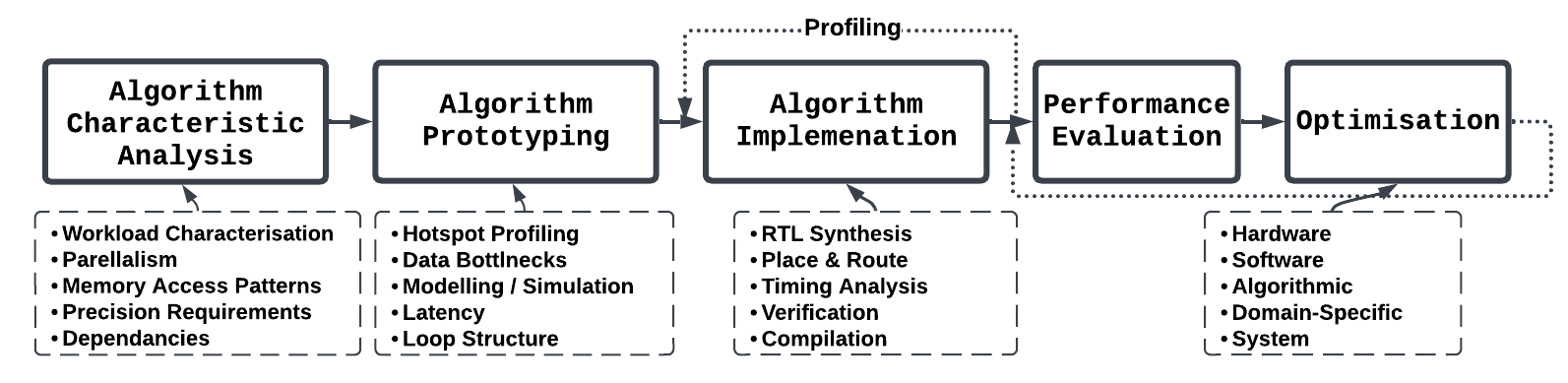
Therefore, To effectively exploit the power of heterogeneous architectures, a robust development flow is crucial. Such a workflow not only aids in pinpointing the optimal architecture but also streamlines the entire development process. As depicted in Fig. 4.2, a comprehensive heterogeneous development pipeline describes a systematic and standardised approach for implementation. This structured flow ensures that developers can seamlessly integrate various computational resources, leverage specialised hardware capabilities, and achieve optimal performance across multiple platforms.

Characteristic Analysis: The first stage involves identifying certain properties of an algorithm discussed in 4.2 and building a model of data, which helps find suitable architectures. Starting with workload characterisation provides a comprehensive overview of the algorithm’s computational and data demands, potentially giving insight into areas where algorithms can be partitioned. Specific algorithms require higher precision, which can impact the choice of the target architecture. However, trading off accuracy for speed is a potential opportunity. Memory access patterns significantly affect cache utilisation and memory latency. It’s important to recognise an algorithm’s parallelism potential while being aware of data dependencies. Moreover, optimising memory access patterns to align with the cache hierarchy can reduce latency and enhance memory throughput. Furthermore, adapting algorithms to harness specific hardware features, such as GPU threads, FPGA pipelines, or TPU matrix multiply units.

Prototyping: This stage involves prototyping designs to identify the initial performance of an architecture to establish a baseline benchmark. Profiling code is done to identify performance bottlenecks, which offers valuable insights into areas suitable for performance enhancement across various architectures. Profiling aims to uncover the ’hotspots,’ sections of code where execution time and resource consumption are disproportionately high. In addition, identifying task, data parallelism or pipelining opportunities which benefit certain accelerators. It is essential to pinpoint potential latency issues, both in I/O operations and within memory, which can arise from slow data transfers or inefficient data handling. Identifying loop structures is important for performance; branching within loops in parallel or pipelined processors can negatively affect performance. This is because branching can lead to divergence, where different execution paths are taken simultaneously, causing processing cores to remain idle. Loop unrolling is a common optimisation technique that can mitigate the effects of branching by increasing the number of operations in each loop iteration, reducing the loop’s overhead. However, if a loop cannot be unrolled or tiled, it may be more efficient to execute the algorithm on a higher clocked sequential core, which can handle branching.

Implementation: After selecting the appropriate architecture for an algorithm, the next step involves its implementation. Depending on the chosen accelerator, this process may entail simulating and synthesising designs and conducting thorough verification. Finally, timing analysis involves evaluating the propagation delays of signals through the circuit’s logic gates and interconnects to ensure they meet the constraints set by the clock cycle time. This helps in detecting and addressing potential timing violations. General-purpose architectures will use compilation methods to high-level code into machine-level instructions tailored for the instruction driven accelerators.

Evaluation & Optimisation: Post-implementation, performance tuning and optimisation techniques are applied to ensure the algorithm runs efficiently, maximising the hardware’s potential. Optimisations can be grouped into four categories: hardware, software, domain-specific and algorithmic. Hardware optimisations involve fine-tuning specific hardware configurations or datatypes such as quantisation or bit-width adjustments. Software optimisations are usually applied at the code level either manually or automatically by compilers. These techniques can include inlining, dead code elimination, and vectorization. Domain-specific is tailored for specific application areas such as downsampling or separable filters. Lastly, algorithmic focus on mathematical refinement to reduce complexity and use more efficient data structures. It’s also necessary to validate the implementation against reference data-sets to ensure functional correctness. Throughout this process, continuous profiling helps identify bottlenecks and areas for further optimisation.

Benchmarking Methodology

This section introduces two benchmarking strategies, micro and macro, each offering distinct approaches to evaluate accelerator performance. While micro-benchmarking focuses on assessing individual algorithms or pipelines, macro-benchmarking provides an overall view by analysing fundamental operations found in many algorithms within the ISP pipeline.

Micro Benchmarking Algorithms

Image processing pipelines contain many operations varying in complexity. For a comprehensive set of results, many popular individual ISP algorithms are chosen to be benchmarked, listed in Table [tab:algorithms] and visually shown in Fig. 4.3. The algorithms, Addition, Subtraction, Erode, Dilate, Box Filter, Gamma Correction, Linearization, and Demosaicing are chosen because they represent foundational operations in image processing. These algorithms exhibit diverse memory access patterns, computational intensities, and parallelism levels. Their inclusion ensures a comprehensive evaluation of an architecture’s capability to handle point-wise and neighbourhood operations.

Complete Imaging Pipelines

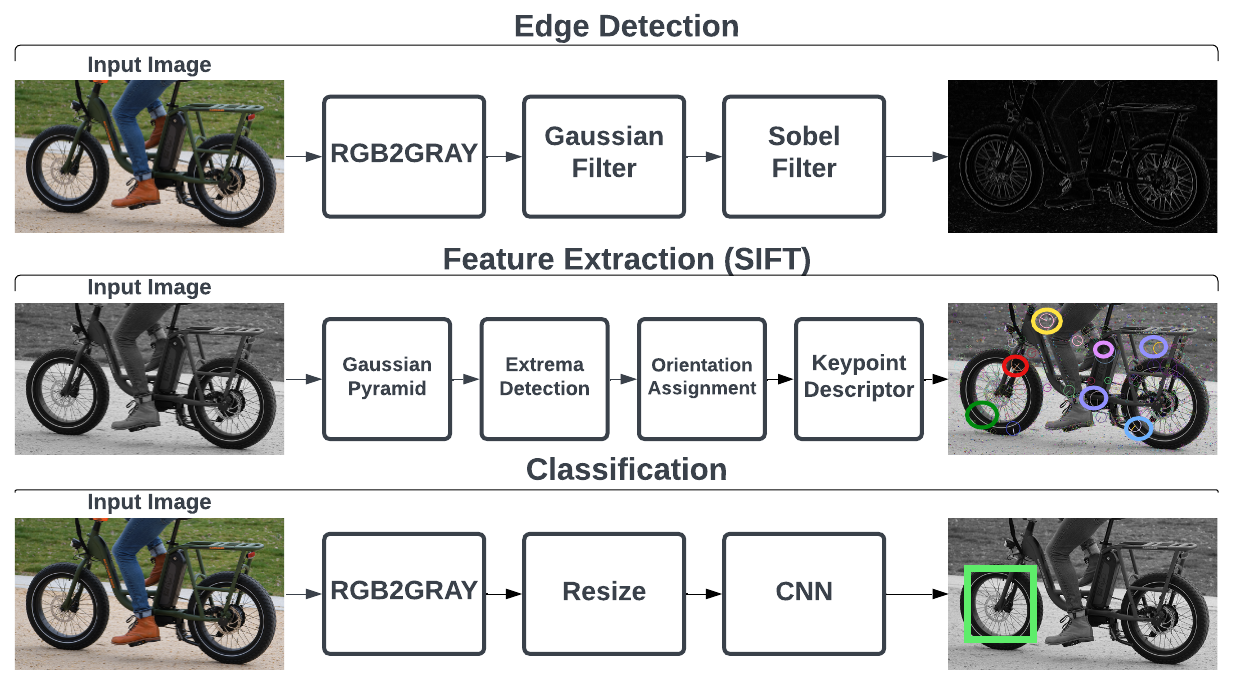
Vision applications usually do not consist of one algorithm but contain many pipelined together to form a complete system. In developing the proposed framework, three exemplars were selected: 1) Edge Detection, 2) Feature Extraction (SIFT) [138] and 3) Classification, representing low to high-level complexity shown in Fig. 4.4. They are partitioned into nine sub-algorithms, namely, RGB2Grey, Gaussian Filter, Sobel Filter, Gaussian Pyramid, Extrema Detection, Orientation Assignment, Descriptor Generation, Resize, and CNN. The sub-algorithms are common building blocks of many other image processing algorithms with varying complexity and therefore are good candidates for benchmarking. For example, Gaussian Pyramid is useful for analysis across different spatial scales and Extrema Detection operations are often used in corner detection and image blending algorithms.

The first pipeline is the edge detection pipeline, designed to identify and emphasise edges within images. It starts with the conversion of RGB colour information into greyscale, a method aimed at reducing redundant processing. Following this, Gaussian filtering is used to achieve image smoothing and noise reduction, essential for accurate edge detection. The Sobel edge detection algorithm, serving as the final stage within this pipeline, detects edges by highlighting abrupt changes in pixel intensities.

The feature extraction pipeline captures important features present within images. The first step in the pipeline involves the construction of a Gaussian pyramid, accomplished by generating multiple versions of the input image through Gaussian filtering and downsampling. This pyramid plays a critical role in identifying features across varying scales. Subsequently, extremum detection is executed, facilitating the identification of keypoints or points of interest within the image. These keypoints serve as reference points for subsequent analysis and interpretation. Grayscale images is used as a input for their simplicity in processing and their robustness to changes in illumination.

The classification pipeline can be found in many deep learning based applications, including vision. It begins with the conversion of RGB to greyscale and subsequently, the image resizing operation is performed to standardise dimensions, ensuring compatibility with the CNN architecture. The final stage involves the application of the CNN algorithm, a state-of-the-art deep learning technique known for its proficiency in tasks related to image classification, object detection, and segmentation.

Macro Benchmarking Algorithms

Many image processing algorithms share foundational operations, which can be used to benchmark accelerators to gain better insight. This section reviews a range of algorithms and their properties that make it an ideal case study for evaluation.

Sustainable Memory Bandwidth in High Performance Computers

Stream memory benchmark[141] (STREAM) is a widely used performance evaluation tool for measuring memory bandwidth in computer systems. It assesses the speed at which a system can read and write data to memory. The benchmark primarily focuses on four memory access patterns: Copy, Scale, Add, and Triad. In the Copy pattern, data is read from one memory location and written to another. The Scale pattern involves reading data, scaling it by a constant, and writing it to a different memory location. The Add pattern reads two arrays, adds corresponding elements, and writes the result to a third array. Finally, the Triad pattern combines scaling and addition operations. The benchmark generates a set of memory performance metrics, including the memory bandwidth, calculated as the amount of data transferred per unit time, typically in gigabytes per second (GB/s). The memory bandwidth (B) can be calculated using the following equation: \[B = \frac{N \times S}{t}\]

where \(N\) is the number of data elements accessed in the memory, \(S\) is the size of each data element in bytes, and \(t\) is the time taken to complete the memory operation in seconds. This equation gives us the memory bandwidth in bytes per second. Image processing is very memory-intensive due to the large amounts of data associated with higher resolution images and the need for frequent data access during processing. Each pixel requires multiple bytes of storage, and when processing, these pixels often need to be accessed multiple times, especially in operations like convolution, filtering, or transformations. The STREAM benchmark becomes invaluable in this context, as it provides insights into how efficiently an architecture can handle the memory demands of image processing tasks.

Fast Fourier Transform

Fast Fourier Transform (FFT) is an algorithm that finds extensive applications in signal processing, image analysis, and various fields where frequency domain analysis is essential. In image processing, FFT is particularly valuable for transforming an image from its spatial domain representation to its frequency domain representation. This transformation enables the identification of various frequency components present in an image, offering insights into patterns, textures, and other intricate details that may not be as evident in the spatial domain.

The FFT algorithm computes the Discrete Fourier Transform (DFT) of a signal in an efficient manner, reducing the computational complexity from \(O(n^2)\) to \(O(n \log (n))\), where \(n\) is the number of data points in the signal. In the case of a 2D image, the FFT operation involves applying the DFT algorithm separately to both the rows and columns of the image’s pixel values. The 2D FFT of an image \(I(x, y)\) is expressed as:

\[F(u, v) = \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} I(x, y) e^{-j 2 \pi \left(\frac{u x}{N} + \frac{v y}{M}\right)}\]

Here, \(F(u, v)\) represents the frequency components in the transformed image, N is the number of pixels along the x-axis, \(M\) is the number of pixels along the y-axis, and \((u, v)\) are the spatial frequency coordinates in the frequency domain.

The resulting 2D FFT representation provides valuable information about the image’s frequency content. Low-frequency components (corresponding to slow changes in intensity) are typically located near the centre of the frequency domain representation. High-frequency components (corresponding to rapid changes in intensity, edges, and textures) tend to be found towards the corners. By analysing this transformed image, practitioners can perform tasks like filtering, denoising, compression, and other frequency-based manipulations to enhance or extract specific features from the original image.

Convolution (Matrix Multiply)

The two most common methods for convolution are general matrix multiply (GEMM) and direct convolution. GEMM-based convolution relies on the im2col algorithm[142], which results in a large memory footprint and reduced performance. Alternatively, direct convolution has a lower memory footprint but the performance is reduced due to the irregular memory access patterns. GEMM can be can be expressed through Eq. ([eq:GEMM]):

\[\label{eq:GEMM} C_{ij} = \sum_{k=1}^{K} A_{ik} \cdot B_{kj}\]

Here, \(C_{ij}\) refers to the element positioned at row \(i\) and column \(j\) within the resultant matrix \(C\), \(A_{ik}\) signifies the element situated at row \(i\) and column \(k\) in matrix \(A\), and \(B_{kj}\) represents the element located at row k and column \(j\) in matrix \(B\). The summation spans across the index \(k\) from 1 to \(K\), where \(K\) corresponds to the number of columns in matrix \(A\) (which should equivalently match the number of rows in matrix BB for accurate multiplication). This equation forms the core operation underlying the GEMM benchmark, which orchestrates the calculation of the matrix product between \(A\) and \(B\) to yield matrix \(C\).

GEMM is found in image processing tasks that require matrix operations. For example, convolutional neural networks (CNNs) extensively use matrix multiplications for convolutional layers, and GEMM’s efficiency and parallelism make it highly useful for accelerating these operations. Additionally, transformations, filters, and image manipulations often involve matrix operations, and therefore GEMM’s optimised implementations can significantly enhance the performance of image processing algorithms.

Performance Metrics

This section focuses on evaluating implemented image processing algorithms using two key metrics: execution time and power consumption. The analysis provides insights into the strengths and limitations of the image processing algorithms on a heterogeneous architecture.

Execution Time

In evaluating the performance of image processing algorithms, precise time measurements are essential to capture the subtle differences across hardware platforms. For the CPU, the C++ standard library’s \(high\_resolution\_clock\) is employed, offering a fine-grained temporal resolution suitable for capturing in microseconds. This method involves marking the start and end times surrounding the algorithm’s execution and computing the difference to determine the elapsed time. On the GPU side, CUDA events were utilised to measure the time taken for the algorithms to run. CUDA events are specifically designed to capture start and end times in a GPU’s environment, ensuring accurate timing measurements that account for the asynchronous nature of GPU operations. Irrelevant processes are stopped within the operating system to prevent interference during the timing measurement. For the FPGA evaluations, the behavioural simulation timing feature of the Vivado software is used. This tool provides a detailed timing analysis, simulating how the algorithm would perform on the FPGA, thereby offering insights into its expected real-world performance. The implementations are written in C/C++/Verilog and uses the time function built into Linux and system performance monitor to measure the runtime of CPU/GPU/FPGA.

Power Consumption

Accurate power estimation is always challenging for software tools. However, systematic steps are taken to minimise assumptions for better accuracy. The approach used to measure the power consumption for the CPU and GPU is obtained by using HWMonitor software. The power is initially measured to determine the average base operating power. Then, each algorithm is executed multiple times, and the power is measured during algorithm runtime. The FPGA on-chip power consumption is measured using the reports from the power analyser feature integrated into Vivado Design Suite. The heterogeneous implementation power consumption is calculated using both HWMonitor and Xilinx’s System Monitor IP. Static power consumption, refers to the constant energy usage of a device when it’s idle, whereas dynamic power consumption varies based on the workload or activity levels, resulting in fluctuations in energy usage

Measurement Environments

While FPGA can provide an accurate execution time in the simulation mode, the same is not true for the CPU/GPU accelerators, as there might be other software (including part of the operating system) competing for compute resources. To mitigate this, the execution time for each bench-marked algorithm is measured as the average of 1,000 iterations on CPU/GPU and closing all other non-core application processes before execution. The Nvidia (CUDA) GPU also has an initialisation time often associated with setting up the GPU context and memory allocations, can be significant, especially for smaller tasks. The initialisation time is recorded for both with and without.

Software & Hardware Environments: OpenCV and Pytorch library is used to implement image processing algorithms and CNNs on CPU and GPU platforms. The FPGA implementation is written in Verilog, using Vivado Design Suite 2019.2. Additionally, for comparison purposes, implementation was done with high-level synthesis (HLS) code using Xilinx Vitis 2019.2. Programmability and flexibility vary across architectures shown in Table [tab:CombinedEnvironment]; CPUs and GPUs are general-purpose, which makes them highly programmable for a wide range of tasks, with languages like C++ being commonly used. FPGAs are more inflexible since significant time is needed to change implementation designs and are typically crafted in hardware descriptor languages such as Verilog. The hardware setup consists of a desktop PC running a Linux operating system, with a discrete GPU and FPGA connected via a high throughput PCIe interface to reduce data latency.

Measurement Approach

The algorithms are implemented individually on each hardware and then combined to create the combined pipeline. For a fair comparison, open-sourced (OpenCV) and CNN libraries(Pytorch) were employed, which are highly optimised for their respective architectures. This is with exception of the Verilog implementations that were developed manually. The parameter for each algorithms used float precision and \(5\times5\) kernel size. During the benchmarking, for consistency, an uncompressed \(8\) bit \(1920 \times 1080\) greyscale (Colour for RGB2Gray algorithm) bitmap image for all experiments and a bayerRAW equivalent for Demoasiacing algorithm.

We provide multiple performance indicators to compare between architectures. For each algorithm, the runtime is measured on each hardware to determine which accelerator executed the operation in the least amount of time. The results from the runtimes are used to calculate the estimated throughput using Eq. ([eq:flop]). The clock cycles per operation (CPO) in Eq. ([eq:ClockComplete]) gives insight into the average number of cycles required to execute an instruction. To have a fair comparison across the target hardware, the energy per operation is normalised using Eq. ([eq:energyepo]): \[\text{Throughput} = \frac{N}{t} \label{eq:flop}\]

\[\text{CPO} = \frac{f \times t}{N} \label{eq:ClockComplete}\]

\[\text{EPO} = \frac{P \times t}{N} \label{eq:energyepo}\]

In these equations, \(N\) denotes the number of operations performed and \(t\) signifies the runtime of the computational task in seconds. \(f\) represents the frequency of the processing unit in hertz, and \(P\) is power consumption in watts.

Experiments, Results & Discussion

This section presents the bench-marked results of each algorithm described in 4.3 and an in-depth discussion. The section is divided into two parts, which include the runtime, power consumption, EPO and throughput results for individual ISP algorithms and combined exemplar pipelines.

Individual ISP Algorithms

Fig. 4.5 & Fig. 4.6 plots the execution time (in milliseconds) and power consumption (in Watts) of the selected benchmarking image processing algorithms varying in complexity across different hardware architectures: CPU, GPU, FPGA, and high-level synthesis implementation on FPGA. The results reveal runtime variations among the architectures for each algorithm. Overall, the CPU performs competitively with the GPU, FPGA and HLS for lower complexity algorithms cases such as RGB2GRAY algorithm, Addition, and Subtraction. It’s evident that algorithms involving a small number of operations, such as colour channel conversion, do not require many computational cores to leverage parallelism or memory access requirements. However, the CPU’s performance starts to decline as the complexity of the algorithms increases, as seen in cases like Sobel, Gamma Correction, GEMM, and FFT, where the large array processing capabilities offered by the GPU and FPGA become more prominent. On average, the CPU is \(4.5\times\) and \(4.35\times\) slower than the GPU and FPGA, respectively.

Across most algorithms, the GPU consistently demonstrates its capability for calculations that require a great amount of multiply and accumulate operations such as GEMM where its vast number of cores are fully occupied. Although FPGAs also contain many processing blocks, their quantity is typically far fewer than GPUs, thus having a small increase in runtime. The results show that GPU implementations outperform FPGAs for larger data/kernel sizes but underperform for smaller sizes where the memory latency and kernel initialisation overhead become significant.

Non-linear algorithms such as Median, Erode and Dilate have a significant impact on all architectures due to having unconventional operations which do not have specialised hard blocks to compute them. In addition, branching conditions involve irregular memory access patterns. The impact can be seen from the GPU and FPGA results, which jump in runtime from linear to non-linear filters where parallelisation is inhibited and the kernel is not separable. The Gamma Correction is another non-linear algorithm which operates on a pixel-wise basis, modifying pixel intensities based on their original values and gamma factors. Division operations are generally more complex and relatively slower compared to multiplication and addition but can be pipelined in hardware. Therefore reducing the overall runtime on all architectures and requiring more resources to compute. The HLS implementation proved competitive in runtime with the hand-written FPGA and GPU for many low-medium complexity algorithms in which the compiler can leverage pre-written functions or libraries. On the contrary, algorithms such as Gamma Corr. or Demosiacing, which are implemented without using pre-optimised libraries, required more compiler effort to generate HDL, resulting in slightly slower execution times.

Related to power consumption, the CPU consumes the most energy in all cases. As the algorithm complexity increases, more power is consumed. The FPGA and HLS are 27% and 7.5% more energy efficient than the GPU in nearly all algorithms, which reveals that direct hardware designs have much less power overhead than the GPU, which needs to support other processes such as host communication. Table [tab:average_reduction_ratios] presents average reduction ratios for each algorithm relative to CPU energy consumption. The GPU exhibits a higher energy reduction ratio in White balance, Sobel, Gamma and GEMM, which reveals that the higher clocked GPU can execute the algorithms faster while offsetting the higher operating power consumption.

The algorithm throughput and energy per operation in nanoJoules, are shown in Fig. 4.7 and Fig. 4.8. Using nJ, as opposed to watts, offers a more granular and clearer measurement. The trend remains, with CPU lagging in throughput and EPO compared to the other architectures for all algorithms. Although in RGB2GRAY, Median & FFT, the CPU is closer to the other accelerators in both metrics due to lower complexity, input size and non-linearity of the algorithms, which don’t map well to highly parallel hardware. The GPU consistently maintains its higher throughput capabilities, as shown by the graphs and lower energy per operation on larger data sized algorithms. The FPGA achieves closer results to the GPU, but being clocked lower and having fewer processing cores results in a slight performance decrease. The HLS tool exhibits comparable performance, closely trailing the GPU and FPGA in most algorithms. Although it experiences a slight performance lag which is attributed to challenges in hardware translation, this setback is mitigated by leveraging optimised pre-written functions used in STREAM. In such algorithms, the HLS tool demonstrates comparable throughput performance to hand-optimised FPGA implementation.

Combined ISP Pipelines

The combined image processing pipeline algorithm for execution times is reported in Fig. 4.9. The runtime results indicate nearly a \(3.46\times\), \(2.92\times\), and \(1.79\times\) order of magnitude improvement going from CPU to GPU, FPGA, and HLS, respectively. The GPU also has a slightly marginal \(\sim0.56\times\) runtime improvement over the FPGA implementation and is closer to a double order of magnitude improvement than the HLS. The memory transfer results in the table show that the latency for each algorithm ranges from \(20\sim70\)ms for the CPU and GPU. In contrast, the FPGA can take advantage of stream processing pixels to minimise memory access for most algorithms.

In the execution time of Edge Total and CNN Total pipelines, the improvement between accelerators is minimal in comparison to the SIFT Total, which has substantial differences between each platform. The Gaussian Pyramid stage within SIFT has the largest contribution to overall SIFT Total execution time. The result can be attributed to image filter algorithms with many multiply-and-accumulate operations, which map well to the parallel processing of GPU and FPGAs due to their high number of compute cores. In contrast, the CPU suffers due to the lack of processing cores where parallelism is needed, resulting in poorer execution time. In addition, the power consumption results in Fig. 4.10 indicate that the FPGA consumes \(1.4\sim 6\)x less power in the Gaussian Pyramid stage than the CPU and GPU, with the HLS implementation being slightly less power efficient. The architecture of FPGAs enables tight-knit designs without additional power consumption by other support functions. Furthermore, the efficiency is evidenced in the Sobel algorithm; the FPGA makes use of the DSP blocks, which consumes less power, although the algorithm contains more than double the numerical operations than Box or Gaussian.

Energy Consumption & Throughput Results

The plots in Fig. 4.11 & Fig. 4.12 show the throughput and energy consumed per operation. The throughput difference between each accelerator for low complexity/arithmetic algorithms such as R2G was consistent, with all three accelerators are comparable. However, the gap widens between CPU and the other hardware in throughput from Gaussian to CNN Total. Comparing GPU and FPGA implementations, the FPGA outperforms in throughput for Edge Total. The hand-written FPGA is able to stream algorithms more effectively than the GPU without overhead CPU memory management latency. Furthermore, the core initialisation and allocation of the GPU does not offset the time it processes for the Gaussian and Resize algorithms.

The GPU and both FPGAs consume \(\sim2\)x less energy per operation compared to the CPU for Gaussian Pyramid, Extrema, Orientation algorithms. This result is because many cores are at full occupancy which start to compute more data in parallel thus increasing throughput. The HLS implementation of Orientation and Descriptor found in SIFT algorithm has worse energy consumption per operation than the hand-written FPGA and GPU. The throughput loss in the descriptor algorithm for GPU and FPGA is due to high data dependency, which leads to sequential processing. In some algorithms, the GPU consumes less energy per operation than the FPGA. The lower power consumption is due to processing the algorithm faster on the GPU than the FPGA to offset the high energy usage from the clock speed and support functions. Table [tab:Result Summary] summarises the results of each calculation (Throughput, CPO, Energy Consumption per Operation).

Discussions

The results highlight the areas where there are clear performance gaps in the implementations on each accelerator. For example, the HLS may not be the best approach to implement all algorithms due to the compiler not optimally translating custom C++ code to Verilog, resulting in performance degradation compared to hand-written FPGA code. Therefore, our benchmarking framework contains a consistent set of metrics to assess various implementations and understand the trade-offs between each target hardware. The results from the framework indicate two generic conclusions: 1) FPGAs are better suited to meet power budget, whereas GPUs can achieve faster execution time (as anticipated), and 2) most optimised performance can be achieved through heterogeneous computing, especially in real-time imaging.

For example, in implementing SIFT, the sub-algorithms Gaussian Pyramid and Descriptor Generation are better suited to GPUs due to faster execution time and throughput, whereas Extrema Detection and Orientation are worthy of targeting FPGAs due to their energy consumption profile. For the first two, GPU consumes \(\sim\)1 & \(\sim\)8 nanoJoule more energy per operation, respectively, but in trade for significant speedup. On the contrary, the latter ones are closely comparable using the throughput and execution time metrics on the GPU and FPGA. However, the power consumed per operation for both algorithms is significantly lower for the FPGA, and hence, the FPGA is better suited. Therefore, partitioning SIFT to target a heterogeneous architecture would benefit from both power and speed performance improvements. However, it is worth noting that such partitioning will incur the cost of frequent memory transfer between architectures.

In the case of the edge detection pipeline from RGB2GRAY to Sobel, the GPU is \(\sim2\)x faster than the FPGA but at the cost of more energy consumption. Therefore, it may be ideal to select the FPGA platform, especially within an embedded system with low power constraints. Furthermore, the low latency of FPGAs would achieve better execution time if the GPU initialisation and memory transfer time are taken into account. Therefore, when considering the deployment of an algorithm on a GPU, it’s vital to ensure that the speedup gained from the GPU’s parallel processing capabilities outweighs this initial transfer overhead. If the algorithm doesn’t run sufficiently fast on the GPU to compensate for this initialisation time, it might not be the optimal choice for real-time or low-latency requirements. In such cases, relying on low-latency architectures such as FPGA offers better overall performance. This highlights the importance of a holistic evaluation of execution times, factoring in initialisation and processing time, before deciding on the accelerator. Additionally, GPUs require a CPU to allocate tasks and manage memory which means additional idle power being consumed.

In the CNN pipeline, the FPGA computes the RGB2GRAY and Resize faster than the other architectures but is \(1.45\times\) slower in CNN inference compared to GPU. However, when considering power consumption and image transfer latency, it is better to pipeline all the operations on an FPGA. The GPU may be better suited to training models or executing larger CNNs that are too big to fit onto FPGA logic. The hand-written FPGA is highly sensitive to implementation and optimisations but allows more granular control over design, while GPUs benefit from a mature ecosystem of compilers and tools. These compilers can automatically optimise and implement core operations, often with high efficiency.

In terms of qualitative visual quality, images processed by CPU, GPU, and FPGA all appear similar since the precision is kept the same for each algorithm. However, for a more comprehensive assessment, deeper analysis can be conducted using visual metrics algorithms (e.g., SSIM, RSME) or through human-based visual experiments.

Conclusions

This chapter discusses the importance of understanding the properties of image processing algorithms to determine which hardware accelerator is suitable and if it can benefit from heterogeneous architecture, especially for real-time vision applications. To facilitate such insight, a benchmarking framework is proposed to observe the features of image processing algorithms and provide a consistent set of metrics to identify trade-offs in performance and energy efficiency of various hardware accelerators, including CPUs, GPUs and FPGAs. We selected commonly used low, medium and high-level image processing operations as exemplars, dissected them in sub-algorithms, and benchmarked their throughput and energy consumption profiles on each hardware. The results indicate that partitioning algorithms based on their memory latency, energy consumption and throughput profiles have the potential for efficient deployment on heterogeneous hardware in achieving optimised performance at a lower power.

The performance variations are influenced by factors such as parallelism, memory access patterns, and the capability of each architecture to map algorithmic operations efficiently. Algorithms that contain large data size parallel operations and have regular memory access patterns tend to perform well on GPU, while FPGA and HLS architectures may perform better for smaller data sized operations. However, both face challenges optimising for irregular memory access patterns and complex algorithmic computations. The FPGA delivers great performance relative to its size, clock and processing resources, but the specialised nature of its architecture is highly sensitive to how the design is implemented. Translating HLS code to hardware can introduce overheads, potentially affecting performance. While HLS tools expedite design cycles, they might not always match the optimisation of manual hardware designs, leading to possible inefficiencies in resource allocation and data paths.

Domain-Specific Optimisations

In recent years, real-time vision systems on embedded hardware have become ubiquitous due to the increased need for different applications such as autonomous driving, edge computing, remote monitoring, etc. Field Programmable Gate Arrays (FPGA) offer the speed and flexibility to architect tight-knit designs that are power and resource-efficient. It has resulted in FPGAs becoming integrated into many applications [143]. Often, these designs consist of many low to high-level image processing algorithms that form a pipeline. Increasingly, the race for faster processing encourages hardware application developers to optimise the algorithms.

Traditionally, optimisations are domain agnostic and developed for general purpose computing. The majority of these optimisations aim to improve throughput and resource usage by increasing the number of parallel operations [144], memory bandwidth [145] or operations per clock cycle [146]. On the contrary, domain-specific optimisations are more specialised in a particular domain and can potentially achieve larger gains in faster processing and reducing power consumption. This chapter proposes domain-specific optimisation techniques on FPGAs that exploit the inherent knowledge of the image processing pipeline.

In demonstrating the proposition, a thorough analysis is presented of well-known image processing algorithms, emerging CNN architectures (MobileNet[147] & ResNet[148]), and Scale Invariant Feature Transform (SIFT) [149]. The decision to include MobileNet is influenced by its popular use within embedded systems, and ResNet is included for its consistently higher accuracy rates compared to other available architectures. Additionally, SIFT is chosen for being the most popular feature extraction algorithm, owing to its performance and accuracy. Algorithmic properties are exploited with the proposed domain-specific optimisation strategies. The optimised design undergoes evaluation and comparison with other general optimised hardware designs regarding performance, energy consumption, and accuracy. The main contributions of this chapter are:

Proposition of four domain-specific optimisation strategies for image processing and analysing their impact on performance, power and accuracy; and

Validation of the proposed optimisations on widely used representative image processing algorithms and CNN architectures (MobilenetV2 & ResNet50) through profiling various components in identifying the common features and properties that have the potential for optimisations.

Domain-Specific Optimisations

Image processing algorithms typically form a pipeline with a series of processing blocks. Each processing block consists of a combination of low, mid, intermediate and high-level imaging operations, starting from colour conversion, filtering to histogram generation, features extraction, object detection or tracking. Any approximation and alteration to the individual processing block or the pipeline have an impact on the final outcome, such as overall accuracy or runtime. However, depending on the applications, such alterations are expected to be acceptable as long as they are within a certain error range (e.g., \(\sim \pm 10\%\)).

Many image processing algorithm operations share common functional blocks and features. Such features are useful for forming domain-specific optimisation strategies. Within the scope of this work, image processing algorithms are profiled and analysed to enable potential areas for optimisations. However, such optimisations impact algorithmic accuracy and therefore, it is important to identify the trade-off between performance, power, resource usage, and accuracy.

The hypothesis suggests that understanding of domain knowledge, e.g., processing pipeline, individual processing blocks, or algorithmic performance, can be used for optimisations to gain significant improvements in runtime and lower power consumption, especially in FPGA-based resource-limited environments. Based on the common patterns observed in a variety of image processing applications, this section proposes four domain-specific optimisation (DSO) approaches: 1) downsampling, 2) datatype, 3) separable filter and 4) convolution kernel size. However, on the flip side, optimisation often leads to lower accuracy in return for gains in speed and lower energy consumption. The effectiveness of these optimisations is compared against benchmark FPGA, GPU and CPU implementations, showing the impact on accuracy. Within the scope of this thesis, four optimisation strategies have been identified and are discussed below:

Optimisation I: Down Sampling

Down/subsampling optimisation reduces the data dimensionality while largely preserving image structure and hence accelerates runtime by lowering the number of computations across the pipeline. Sampling rate conversion operations such as downsampling/subsampling are widely used within many application pipelines (e.g., low bit rate video compression [83] or pooling layers in Convolutional Neural Network (CNN) [150]) to reduce computation, memory and transmission bandwidth. Image downsampling reduces the spatial resolution while retaining as much information as possible. Many image processing algorithms use this technique to decrease the number of operations by removing every other row/column of an image to speed up the execution time. However, the major drawback is the loss of image accuracy due to removing pixels. down sampling optimisation used for each selected algorithm is a bilinear interpolation, and both runtime and accuracy are measured.

Bilinear downsampling is a technique that reduces the number of pixels in an image by computing each output pixel as a weighted average of its four nearest input pixels. The weights, represented by interpolation factors \(\alpha_i\) and \(\beta_i\), are determined based on the distances between the target output pixel \((x, y)\) and the neighbouring input pixels \((x_i, y_i)\) in both the horizontal and vertical directions. These factors contribute to a smoothed, downsampled image by interpolating colour values based on the surrounding pixel information. Mathematically, the value of a downsampled pixel \(D(x,y)\) can be calculated using the following equation: \[D(x,y) = \sum_{i=1}^{4} \alpha_i \cdot \beta_i \cdot I(x_i, y_i)\] Where \(D(x,y)\) represents the downsampled pixel value at location \((x, y)\) in the downscaled image, and \(I(x_i, y_i)\) represents the intensity (colour value) of the neighbouring pixel \((x_i, y_i)\) in the original image. Downsampling reduces the image size between octaves in the ’Gaussian pyramid’ construction stage.

Optimisation II: Datatype

Bit width reduction through datatype conversion (e.g., floating-point (FP) to integer) significantly reduces the number of arithmetic operations, resulting in optimised runtime at lower algorithmic accuracy. Whilst quantising from FP to integer representations is common in the software domain, one of the advantages of reconfigurable hardware is the capability to reduce dimensionality to arbitrary sizes (e.g., 7, 6, 5, 4 bits) as a trade-off between accuracy and power/performance.

Consider an image where each pixel has a floating-point value in the range of \(0\) to \(1\). A straightforward way to perform quantisation is to map these values to a set of integers. One commonly used formula for this conversion is:

\[Q(x) = \text{round}(x \times (2^k - 1))\]

Here, \(Q(x)\) is the quantised value, \(x\) is the original floating-point value, and \(k\) is the bit-depth (e.g., \(8\) for an 8-bit image). The function \(\text{round}\) rounds the value to the nearest integer. This equation multiplies the floating-point value by \(2^k - 1\) (255 for an 8-bit image) and rounds it, converting the value into an integer between \(0\) and \(2^k - 1\). This process significantly reduces the data size and computational requirements, albeit with some loss of information due to rounding. The converted integer values can then be used in place of the floating-point values for further processing tasks.

In image processing, most algorithms are inherently developed using floating-point (FP) calculations. Although FP offers higher accuracy, it comes at the expense of computational complexity and, therefore, increased resource and energy consumption. A viable alternative is fixed-point arithmetic, where a fixed location of the decimal point separates integers from fractional numbers. Opting for fixed-point representation can significantly improve computational speed, albeit at the cost of some accuracy. Here, a datatype conversion optimisation is proposed, wherein all operational stages are converted from FP to integer arithmetic. This conversion allows for an evaluation of the trade-off between performance and accuracy.

Optimisation III & IV: Convolution

Convolution kernel size optimisation reduces computational complexity, which is directly proportional to the squared size of the filter kernel size, i.e., \(\mathcal{O}(n^2)\) or quadratic time complexity. Convolution is a fundamental operation employed in most image processing algorithms that modify the spatial frequency characteristics of an image. Given a kernel and image size \(n \times n\) and \(M \times N\), respectively, convolution would require \(n^2\times M \times N\) multiplications and additions. For a given image, complexity is dependent on the kernel size, leading to a complexity of \(\mathcal{O}(n^2)\). Reducing kernel size significantly lowers the number of computations; for example, replacing a \(5 \times 5\) kernel with a \(3\times3\) kernel would reduce the computation by a factor of \(\times2.7\). Therefore, this is proposed as an ideal target for optimisation, although it may come at the cost of accuracy.

\[\label{eq:Separable} \begin{aligned} \quad \frac{1}{4} \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix} \quad \times \quad \frac{1}{4} \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} = \frac{1}{16} \begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix} \end{aligned}\]

Another convolution optimisation strategy is separable filters, which is a type of linear filter that can be broken down into a series of 1D filters shown in Eq.[eq:Separable], making it computationally efficient for image processing tasks. The separability property stems from the ability to represent a 2D filter kernel as the outer product of two 1D kernels. This means that instead of directly convolving the image with a 2D kernel, one can first convolve it along the rows with a 1D kernel and then convolve the result along the columns with another 1D kernel. The formula for a separable filter can be expressed as:

\[H(x, y) = F(x) \cdot G(y)\]

where \(H(x,y)\) is the 2D filter kernel, \(F(x)\) is the 1D filter kernel applied along the rows, and \(G(y)\) is the 1D filter kernel applied along the columns. By separating the filtering process into 1D convolutions, the number of operations required is significantly reduced, leading to faster image filtering compared to non-separable filters. Common examples of separable filters include Gaussian filters and the Sobel operator for edge detection.

Case Study Algorithms

In this section, an overview of the representative algorithms targeted for optimisation is presented, as discussed in Section 5.1. Subsequently, the proposed optimisations will be applied to enhance their performance.

SIFT

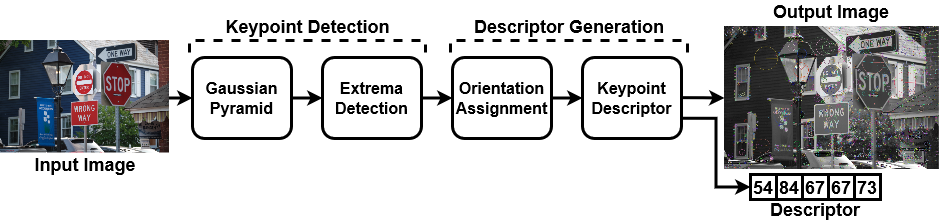
SIFT [149] is one of the widely used prototypical feature extraction algorithms. To demonstrate the proposed optimisations, various versions of SIFT have been implemented, consisting of two main and several sub-components as shown in Fig. 5.1 and described below.

Scale-Space Construction

(a)	(b)

Gaussian Pyramid

The Gaussian pyramid \(L(x,y,\sigma)\) is constructed by taking in an input image \(I(x,y)\) and convolving it at different scales with a Gaussian kernel \(G(x,y,\sigma)\): \[\begin{aligned} \label{eq:SIFT1} G(x,y,\sigma) &= \frac{1}{2 \pi \sigma ^2} e^{- \frac{x^2 + y^2}{2 \sigma ^2}}, \\ L(x,y,\sigma)&=G(x,y,\sigma) * I(x,y), \end{aligned}\] Where \(\sigma\) is the standard deviation of the Gaussian distribution. The input image is then halved into a new layer (octave), which is a new set of Gaussian blurred images. The number of octaves and scales can be changed depending on the requirements of the application.

The implemented block design reads pixel data of input images into a line buffer shown in Fig. 5.2(a). The operations in this stage are processed in parallel for maximum throughput. This is due to significant matrix multiplication operations, which greatly impact the runtime. This stage is the most computationally intensive, making it an ideal candidate for optimisation.

The Difference of Gaussian \({DOG}(x,y,\sigma)\), in Eq.[eq:SIFT3] is obtained by subtracting the blurred images between two adjacent scales, separated by the multiplicative factor \(k\).

\[\label{eq:SIFT3} \textsl{DOG}(x,y,\sigma)=L(x,y,k\sigma)-L(x,y,\sigma).\]

The minima and maxima of the \(DOG\) are detected by comparing the pixels between scales shown in Fig. 5.2(b). This identifies points that are best representations of a region of the image. The local extrema are detected by comparing each pixel with its \(26\) neighbours in the scale space (\(8\) neighbour pixels within the same scale, \(9\) neighbours within the above/below scales). Simultaneously, the candidate keypoints with low contrast or located on an edge are removed.

Descriptor Generation

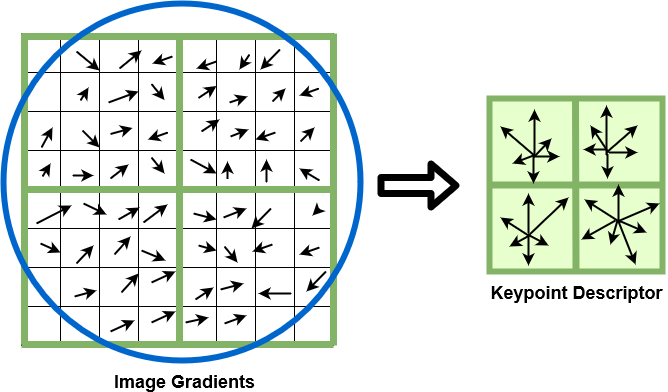
Magnitude & Orientation Assignment

Inside the SIFT descriptor process shown in Fig. 5.3, the keypoint’s magnitude and orientation are computed for every pixel within a window and then assigned to each feature based on the local image gradient. Considering \(L\) is the scale of feature points, the gradient magnitude \(m(x,y)\) and the orientation \(\theta (x,y)\) are calculated as:

\[\begin{aligned} m(x,y) &=\sqrt{L_{x}(x,y)+L_{y}(x,y)}, \\ \theta (x,y) &=tan^{-1}\left ( \frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)} \right). \label{eq:SIFT5} \end{aligned}\] Once the gradient direction is obtained from the result of pixels in the neighbourhood window, a \(36\) bin histogram is generated. The magnitudes are Gaussian weighted and accumulated in each histogram bin. During the implementation, \(m(x,y)\) and \(\theta (x,y)\) are computed based on the CORDIC algorithm [151] in vector mode to map efficiently on an FPGA.

Keypoint Descriptor

After calculating the gradient direction around the selected keypoints, a feature descriptor is generated. First, a \(16\times16\) neighbourhood window is constructed around a keypoint and then divided into sixteen \(4\times4\) blocks. An \(8\)-bin orientation histogram is computed in each block. The generated descriptor vector consists of all histogram values, resulting in a vector of \(16 \times 8 = 128\) numbers. The \(128\)-dimensional feature vector is normalised to make it robust from rotational and illumination changes.

SIFT Hardware Implementation

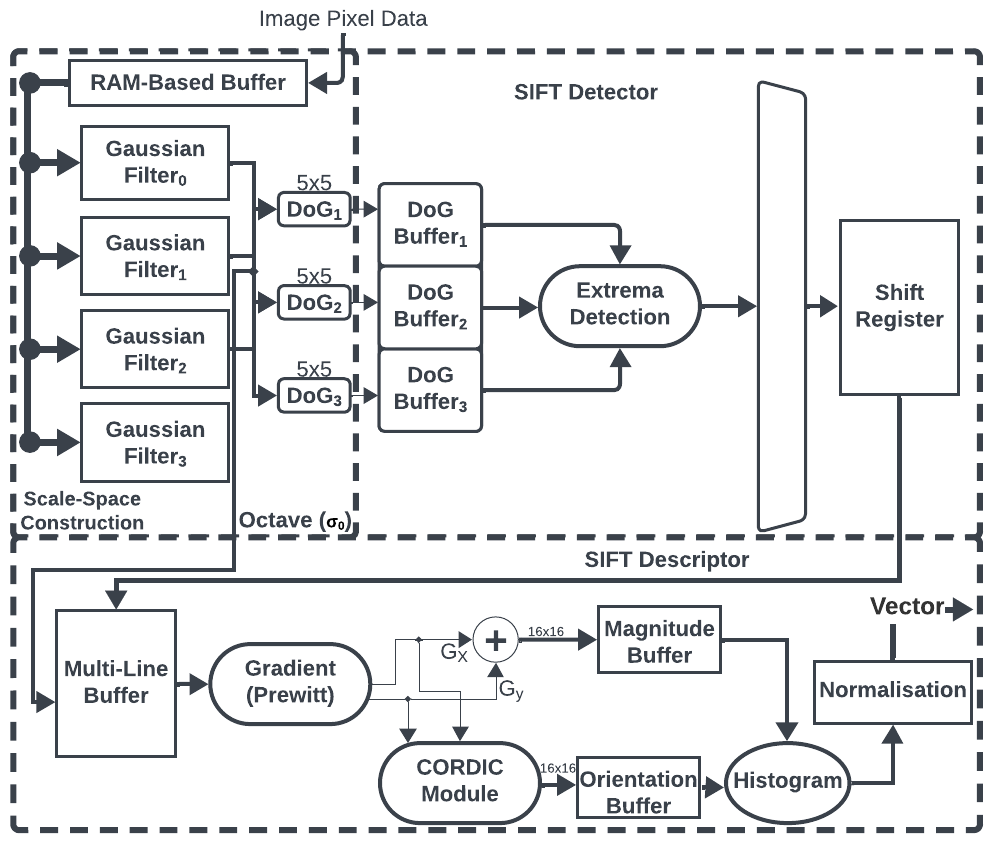
The high-level hardware block diagram depicted in Fig. 5.4 of SIFT illustrates the individual modules that build up the complete algorithm.

Scale-Space Construction:

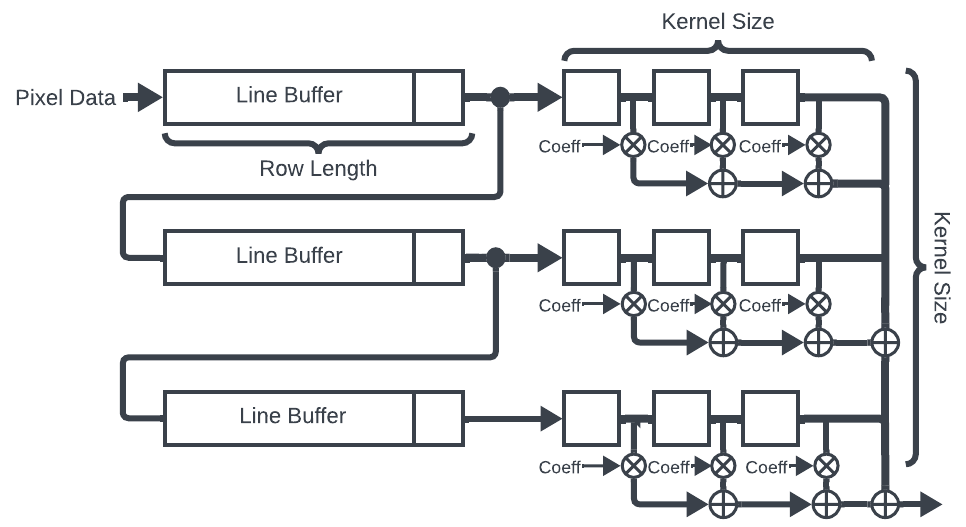
To efficiently process the image data, the Gaussian convolution module observed in Fig. 5.5 uses line buffers to store and process pixel data. As pixel data streams into the FPGA, it is stored in the buffers organised in rows corresponding to image rows. These line buffers hold a portion of the image data needed to compute the convolution operation. Using line buffers, the FPGA can process multiple pixels simultaneously, reducing latency and increasing throughput. Furthermore, pre-calculated coefficients defining the approximated Gaussian weights are applied to the pixel values during filtering and are stored in BRAM registers. The implementation uses separable filters, the module first applies a one-dimensional Gaussian filter in the horizontal direction followed by another in the vertical direction.

In addition, handling boundary pixels is vital to preserve image integrity. However, in this implementation focused on a \(1920\times1080\) image size, boundary pixels are neglected to simplify hardware design.

Subsequently, adjacent levels of the Gaussian pyramid are subtracted from each other to obtain the DoG pyramid. This subtraction operation is preformed in parallel between each scale and the three resulting DoG are buffered. Two row buffers are used for every DoG and form a \(3 \times 3\) neighbourhood for extrema detection. Fig. 5.6 illustrates the design of maxima detector module where each pixel is then compared to its 26 neighbors, and the minimum magnitude is computed to determine the local extremum. Each DoG buffers output consists of three values that constitute one column of a 3x3 neighbouring window. The DoG words are forwarded to a comparator circuit which compares the middle pixel of DoG2 with its neighbours, and an OR gate indicates if it’s an extremum. Note that the first row is processed on the fly without requiring buffers, since DoG operation is a single-pixel operation and doesn’t affect the boundaries. The width of these buffers depends on the range of the DoG operation results.

CORDIC & Prewitt Mask Module:

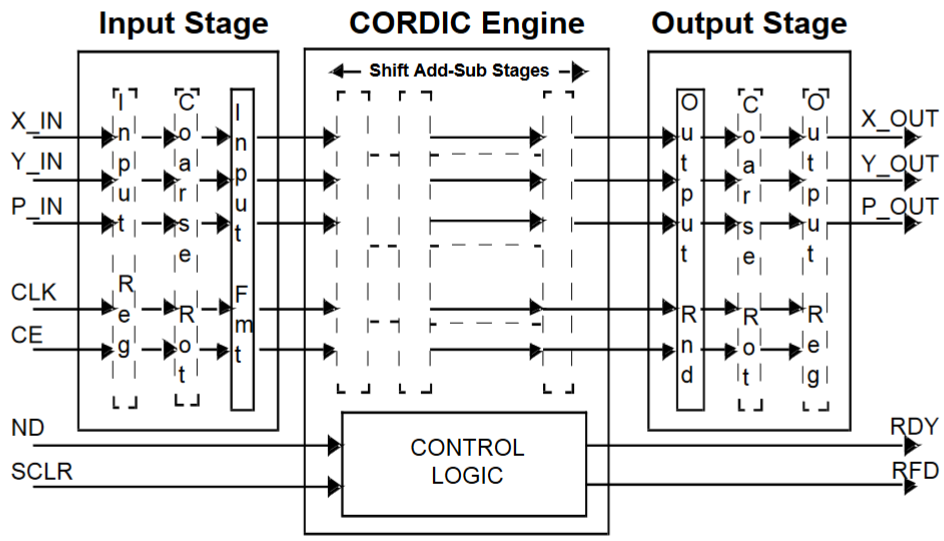
In the proposed implementation, the first derivatives of G2, are produced by applying Prewitt mask operator to generates the first-order derivatives of the image with respect to both the x and y directions. The magnitude is efficiently computed using the sum of absolute values of \(G_x^2\) and \(G_y^2\). This approach replaces the square root operation traditionally used in gradient magnitude calculations. After computation, the result is stored as 8 bits, retaining only the integer part of the magnitude for subsequent calculations. The gradient orientation is computed traditionally by using large Look-Up Tables (LUTs) for precomputed arctangents and hardware resources for division operations. However, the implementation uses Xilinx IP CORDIC module, which solves trigonometric equations iteratively and also computes a broader range of equations, including the hyperbolic and square root. The output orientation assignments are stored as a 6-bit integers.

Histogram & Normalisation Module:

In the SIFT descriptor generation stage, each keypoint contributes to histogram entries representing gradient orientations and magnitudes within a local region. Keypoints may influence multiple orientation bins, leading to limited parallelisation. To address this, the descriptor computation utilises eight BRAMs, each dedicated to a specific orientation bin. These arrays independently accumulates data from keypoints associated with a particular orientation, enabling parallel processing. Keypoint coordinates and orientation information are used to distribute magnitude contributions across the arrays. The non-data dependent nature of each array allows for pipelined accumulation and simultaneous processing of multiple keypoints. After processing all the keypoints, an adder tree sums histogram values stored in the array.

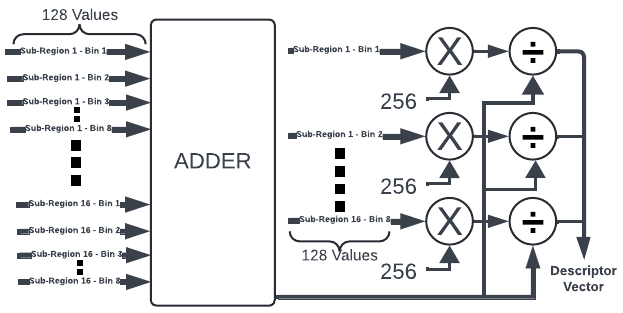
The unnormalised histogram data is streamed into the final module shown in Fig. 5.8 that performs normalisation. The input data is converted into floating point representation, to ensure accuracy and comparability with other hardware architectures. Once, converted the data is stored into BRAM and L1-norm of the histogram is calculated concurrently using DSPs. Each entry in the histogram is subsequently divided by the computed L1-norm, followed by a square root operation. The resulting normalised values are then converted from floating-point to fixed-point representation (8 bit) to minimise storage space. Furthermore, the outputs from each processing element are accumulated into a unified output vector using a combination of FIFO buffers and a multiplexer.

Digital Filters

Digital filters are a tool in image processing to extract useful information from noisy signals. They are commonly used for tasks such as smoothing, edge detection, and feature extraction. Filters operate by applying a kernel, or a small matrix of values, to each pixel of an image. The kernel is convolved with the image, and the resulting output value is placed in the corresponding pixel location of the output image shown in the Eq. ([eq:kernel]). \(I(x,y)\) is the input image and \(K(k_x,k_y)\) is the kernel. The convolution result \(O(x,y)\) is calculated by:

\[\label{eq:kernel} \begin{aligned} O(x, y) &= \sum_{k_x} \sum_{k_y} I(x - k_x, y - k_y) \cdot K(k_x, k_y) \end{aligned}\]

The indices \(k_x\) and \(k_y\) correspond to the coordinates of the kernel \(K\), \(x\) and \(y\) correspond to the coordinates of the output image \(O\).

Convolutional Neural Network

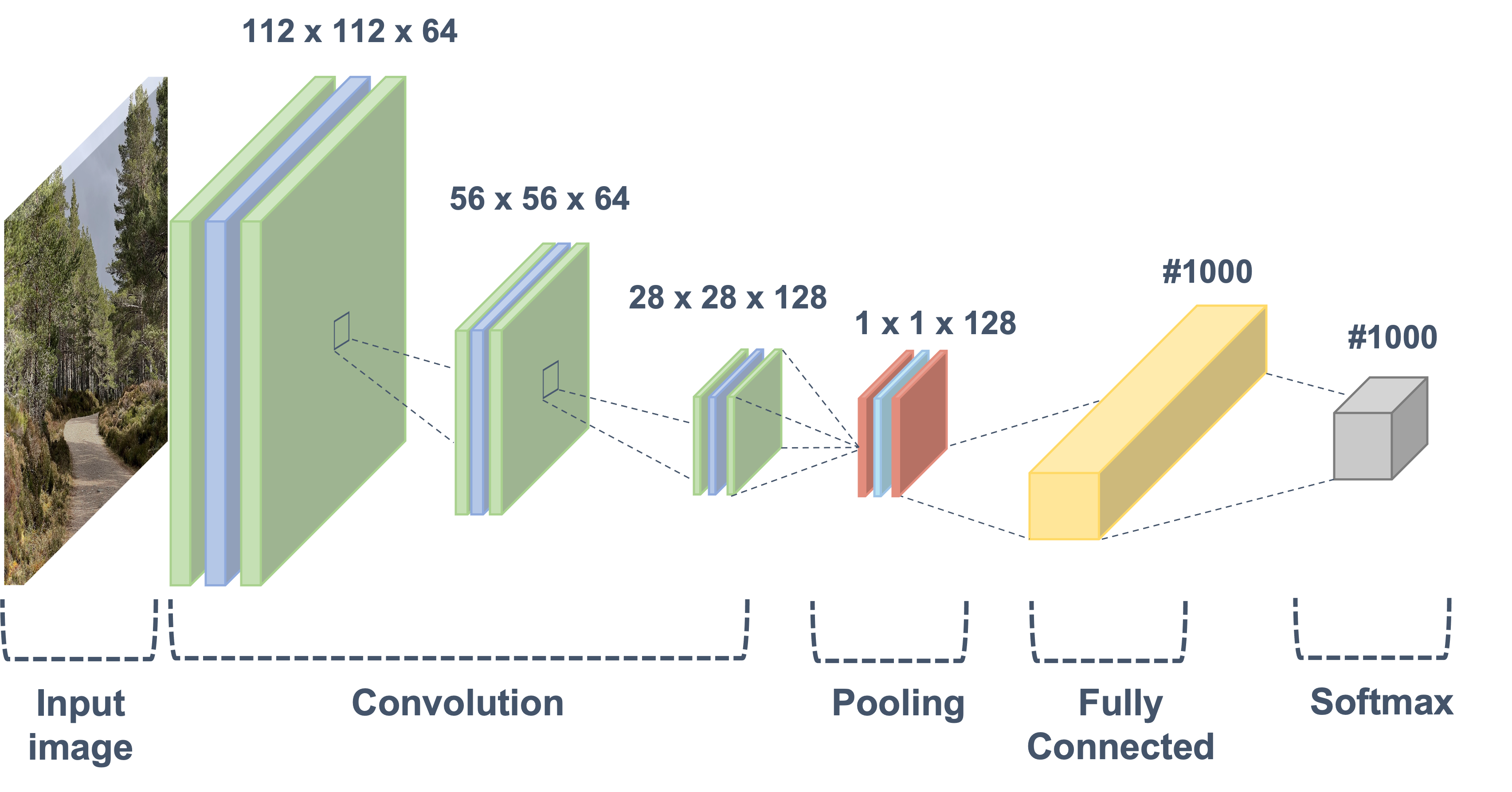
Convolutional Neural Networks are a class of deep neural networks typically applied to images to recognise and classify particular features. A CNN architecture typically consists of a combination of convolution, pooling, and fully connected layers shown in Fig. 5.10.

The convolution layers extract features by applying a convolution operation to the input image using a set of learnable filters (also called kernels or weights) designed to detect specific features. The output of the convolution operation is a feature map, which is then passed through a non-linear activation function, such as ReLU, to introduce non-linearity into the network. The convolutional layers can be stacked to form a deeper architecture, where each layer is designed to detect more complex features than the previous one. In addition, it is the most computationally intensive layer because each output element in the feature map is computed by repeatedly taking a dot product between the filter and a local patch of the input, which results in a large number of multiply-add operations.

The pooling layers are responsible for reducing the spatial size of the feature maps while retaining important information. The most common types of pooling are max pooling and average pooling. These layers typically use a small window that moves across the feature map and selects the maximum or average value within the window. This operation effectively reduces the number of parameters in the network and helps to reduce overfitting.

The fully connected layers make predictions based on the extracted features. These layers take the output from the convolutional and pooling layers and apply a linear transformation to the input, followed by a non-linear activation function. The fully connected layer usually has the same number of neurons as the number of classes in the dataset, and the output of this layer is passed through a softmax activation function to produce probability scores for each class. A CNN architecture also includes normalisation layers such as batch normalisation, dropout layers that are used to regularise the network and reduce overfitting, and an output layer that produces the final predictions.

Experimental Results and Discussion

We verify the proposed optimisations on ’SIFT’, ’Box’, ’Gaussian’ and ’Sobel’ (in Fig. 5.11) algorithms, as well as MobileNetV2 and ResNet50 CNN architectures. This is achieved by creating baseline benchmarks on four target hardware CPU, GPU and FPGA, followed by the realisations of the optimisations individually and combined. The CPU and GPU versions for Filter and SIFT algorithms are implemented using OpenCV[22]. Pytorch library is used to implement CNN architectures (ResNet50 & MobileNetV2) and optimisations. Additionally, both architectures are pre-trained on the image-net classification dataset. The FPGA implementation for all algorithms is developed using Verilog (SIFT/Filter) and HLS (CNN). All baseline algorithms and CNN models use floating point 32 (FP32), and an uncompressed grayscale \(8\)-bit \(1920\times1080\) input image is used for the SIFT algorithm, and each sub-operation is profiled. Details of the target hardware/software environments and power measurement tools are given in Table [tab:HWEnvironment].

Dataset. The input images used in the CNN and Filter experiments are from LIU4K-v2 dataset [153]. The dataset contains 2000 high resolution \(3840\times2160\) images with various backgrounds and objects.

Performance Metrics

As part of the evaluation process, we measure three different performance metrics, namely, 1) execution time, 2) energy consumption and 3) accuracy.

Execution time

The execution time measured for the CPU and GPU platforms uses time function libraries to count the smallest tick period. Each algorithm/operation is run for 1000 iterations and averaged to minimise competing resources or other processes directly affecting the architecture, especially for the CPU architecture. The GPU has an initialisation time which is taken into account and removed from the results. The timing simulation integrated into Vivado design suite software is used to measure the time for the FPGA platform. The experiments exclude the time of both the image read and write from external memory. We compute the frame per second (FPS) as the inverse of the execution time: \[\label{eq:FPS} \text{FPS}= 1/\text{Execution Time}.\]

Power Consumption

Two common methods used for measuring power are software and hardware-based. Accurately estimating power consumption is a challenge using software-based methods, which have underlying assumptions in their models and may not measure other components within the platform. In addition, taking the instantaneous watt or theoretical TDP of a device is not accurate since power consumption varies on the specific workload. Therefore, we obtain the total energy consumed by measuring the power over the duration of the algorithm executed. A script is developed to start and stop the measurements during the execution of the algorithm and extract the power values from the software.

With the use of a power analyser within the Vivado design suite and the MaxPower-tool, the measurement of FPGA power consumption is divided into two parts, (1) static power and (2) dynamic power. Static power relates to the consumption of power when there is no circuit activity and the system remains idle. Dynamic power is the power consumed when the design is actively performing tasks. The power consumption for the CPU and GPU is obtained using HWMonitor and Nvidia-smi software. To have a fair comparison across the target hardware for the SIFT algorithm, we normalise it as the energy per operation (EPO): \[\label{eq:energy1} \text{Energy} = (\text{Power} * \text{Execution Time}).\]

Additionally, We calculate the energy consumption for the Filter and CNN algorithms:

\[\label{eq:energy} \text{EPO} = (\text{Power} * \text{Execution Time})/\text{Operations}.\]

Accuracy

With an expectation that the optimisations impact overall algorithmic accuracy, we capture it by measuring the Euclidean distance between the descriptors generated from the CPU (our comparison benchmark) to the descriptor output produced by the FPGA. The Euclidean distance \(d(x,y)\) is calculated in Eq. ([eq:Euc]) where \(x\) and \(y\) are vectors, and \(K\) is the number of keypoints generated. This accuracy measurement is only used for the SIFT algorithm implementation.

\[\label{eq:Euc} d(x,y)=\sqrt{\sum_{i=1}^{K} (x_{i}-y_{i})^{2}}.\]

Subsequently, the accuracy for each Euclidean distance is calculated using Eq. ([eq:Accu]): \[\label{eq:Accu} \text{Accuracy} = 100 - \left( \left( \frac{\text{Euclidean Distance}}{\text{Max Distance}} \right) \times 100\right)\]

The Euclidean Distance denotes the distance between the two descriptor vectors being compared, and Max Distance represents the maximum Euclidean distance found in the vector. The accuracy is transformed to have 100% indicate identical descriptors, while 0% indicates completely dissimilar descriptors.

We used root mean square error (RSME) to compare the input image to the output images produced by each hardware accelerator to determine the pixel accuracy. RMSE is defined as: \[RMSE = \sqrt{(\frac{1}{n})\sum_{i=1}^{n}(y_{i} - x_{i})^{2}}\] Where the difference between the pixel intensity values of output and input (y_i,x_i) images. Divided by N, which is the total number of pixels in the image.

The accuracy of the CNN architecture is measured by taking the number of correct predictions divided by the total number of predictions:

\[\text{Accuracy} = \frac{\text{Number of Correct Predictions}}{\text{Total Number of Predictions}} \times 100\]

A high accuracy indicates that the model is making accurate predictions, while a low accuracy suggests room for improvement in the model’s performance.

Results and Discussions

The results and discussions section contains the evaluation of algorithms in three categories, feature extraction algorithms (SIFT), filter algorithms (Box, Gaussian, Sobel) and Convolution Neural Networks (MobilenetV2, ResNet50).

SIFT

We obtain results for FPGA implementations of the SIFT algorithm, considering various optimisations or combinations of them. Two sets of results are captured for octave, scale of (2,4) and (4,5) as they are regularly reported in the literature for SIFT implementation on FPGA. The results are primarily obtained at a target frequency of 300 MHz for various components of SIFT and execution time and accuracy are reported in Table [tab:Optimisation_Summary] along with FPS numbers in Fig. 5.12.

In terms of individual optimisations on the base FPGA implementation, down sampling and integer optimisations had the most reduction of accuracy but in trade for a greater reduction of runtime. On the other hand, \(3\times3\) kernel size (down from default \(5\times 5\)) had better accuracy results but with a small improvement on the overall runtime. In the case of combined optimisations, both down sampling and integer combinations greatly reduced the execution times but at a cost of \(8\sim10\%\) accuracy loss. In the most optimised case, (4,5) and (2,4) configurations achieved \(17\) and \(50\) fps, at an accuracy of \(90.18\%\) and \(89.45\%\), respectively. The \(10 \sim 11\%\) loss in accuracy in both configurations can be attributed to the loss of precision and pixel information resulting in imperfection in feature detection.

The comparison with optimised CPU and GPU implementations is shown in Table [tab:platoformsummary] which includes total execution time and energy consumption per operation (nJ/Op). Results indicate the optimised FPGA implementation achieved comparable GPU runtime at 600 MHz but significantly outperformed them when energy consumption statistics are taken into account. The GPU results excluded the initialisation time, which would add greater latency to the overall runtime. In addition, the power consumption of the GPU is at \(12.47\)nJ/Op, which would make it a difficult choice for real-time embedded systems. On the other hand, optimised FPGA implementations have better performance per watt than the GPU and CPU. The comparison with the state-of-the-art FPGA implementations is reported in Table [tab:state_of_art], and results show major improvements in the runtime even with larger image size and more or similar feature points (\(\sim10000\)). Finally, for completeness, we report the resource and power usage statistics for optimised configurations at 300 MHz in Table [tab:resourseusage].

Filter Implementations

Fig. 5.14 & Fig. 5.13 plots the runtime and energy consumption of three image processing filter algorithms (Box, Gaussian, and Sobel) with various optimisations strategies applied to the baseline algorithm. Comparing the baseline performance, the CPU architecture suffers the most in execution time and energy consumption which can be attributed to the lack of many compute cores. In contrast, GPUs and FPGAs exploit data parallelism and stream/pipeline processing to significantly reduce runtime.

Both Fig. 5.14 & Fig. 5.13 show that the performance of both GPU and FPGA are comparable in both metrics studied. The GPU demonstrated a marginally better computation speed compared to the FPGA, with an average execution time improvement of \(9.45\%\) for Box and Gaussian algorithms. On the other hand, the FPGA has a \(5.88\%\) improvement for Separable Filter over GPU.

In the case for Sobel, the FPGA achieves a speedup of approximately \(1.09\times\) over the GPU across all optimisation strategies. The smaller kernel size allows the FPGA to use its DSP slices to efficiently compute the algorithm, whilst the GPU operations do not fully occupy the compute resources available which results in load imbalance and communication latency. Relative to power consumption, the CPU experiences the most significant impact in all cases by consuming \(1.19\times\) Joules on average. The higher energy usage can be attributed to their higher clock, complex memory hierarchy and lack of parallel capability. The GPU has been observed to consume \(\sim1.36\times\) more Joules than the FPGA. The high energy cost can be derived from the base support/unused logic components consuming static power. However, the FPGA operates on the least energy consumed per clock due to its custom-written nature. The energy consumption for seperable optimisation reveals similar results between the GPU and FPGA. This is attributed to the GPU able to compute the algorithm faster to offset the higher clock speed energy cost.

All optimisations, e.g Datatype, Kernel, Downsampling, and Separable Filters optimisations had major improvements for each accelerator. Reducing the kernel size to \(3\times3\) kernel size and applying Separable Filters had the most impact due to lowering the number of operations computed during the convolution operation. The Datatype and Downsampling optimisations had around on average \(12.24\sim28.16\%\) decrease in runtime for all algorithms. The optimisation runtime results and accuracies of each filter algorithm are reported in Table [tab:ImageProcessingAlgorithmOptimisationSummary]. In terms of image accuracy, downsampling has the most significant difference compared to the original, which can be attributed to the rows that are removed due to the algorithm.

CNN Architecture

Fig. 5.15 displays the runtime performances and classification accuracy of the baseline and optimised CNN algorithms on each hardware architecture. The results show that the CPU, GPU, and FPGA exhibit similar levels of performance, with the GPU having an average improvement of \(5.41\sim12\%\) over the FPGA for the Downsampling optimisation in MobileNetV2 and the baseline for ResNet50, respectively. The FPGA leads in the Datatype optimisation over the GPU with a \(6.25-11.1\%\) reduction in time for both CNNs. The Datatype optimisation involves quantisation of the model’s weights from FP32 to 8-bit to reduce complexity. The FPGA computes the quantised operations faster on both architectures due to exploiting the DSP blocks and requiring no additional hardware logic for floating-point arithmetic. However, the quantised model weights are unable to represent the full range of values present in the input image, resulting in a \(\sim10\%\) accuracy loss for all platforms. The Downsampling strategy has a slight improvement in runtime with minimal impact on the accuracy, with a loss around \(\sim5\%\).

In Fig. 5.16, the energy consumption graph shows that the CPU consumes on average, \(3.14\times\) more energy than the other accelerators for both CNNs. In addition, the ResNet50 architecture has more layers than MobileNetV2 and, therefore, contains more operations, resulting in higher energy usage. In all cases, the FPGA consumes the least amount of energy, \(1.11\sim3.55\times\) less than the CPU and GPU, to compute the image classification. The results show the potential of reducing the computation time of CNNs by further applying the proposed optimisations in a layer by layer basis, but at the cost of slight accuracy loss. The optimisation results of each CNN architecture and accuracy are reported in Table [tab:CNNSummaryTable].

Consequently, larger images or complex networks with many layers and larger filter sizes require more memory to store the weights and activations. This leads to higher memory requirements, especially within real-time embedded systems where space is limited. However, applying optimisations can alleviate the computational load, but careful consideration must be taken to understand the trade-offs between runtime and accuracy depending on the application. The Kernel optimisations could not be implemented on the chosen CNN architectures, which would require heavily modifying the standard convolution operation in both networks. This would completely change the network, thus creating a new architecture.

Conclusion & Future Direction

This chapter proposes new optimisation techniques called domain specific optimisation for real-time image processing on FPGAs. Common image processing algorithms and their pipelines are considered in proposing such optimisations, which include down/subsampling, datatype conversation and convolution kernel size reduction. These were validated on the popular image processing algorithms and convolution neural network architectures. The optimisation results for CNN and Filter algorithms vastly improved the computation time for all processing architectures. The SIFT algorithm implementation results significantly outperformed state-of-the-art SIFT implementations on FPGA and achieved runtime at par with GPU performances but with lower power usage. However, the optimisations on all algorithms come at the cost of \(\sim5-20\%\) accuracy loss. Overall, Downsampling and datatype optimisation resulted in the most significant reductions in execution time and energy consumption.

The results demonstrate that applying domain-specific optimisations to increase computational performance while minimising accuracy loss demands in-depth and thoughtful consideration. Furthermore, it should be noted that the optimisations selected in the experiment are non-exhaustive, leaving room for further exploration.

One proposal for algorithms comprising multiple operation stages is to use adaptive techniques instead of fixed integer downsampling factors, bit-widths, and kernel sizes. These adaptive methods analyse the data and dynamically adjust the level of optimisation based on input characteristics. For instance, adjusting the bit-width and downsampling factor according to the specific input data within each stage can yield better results and strike a more suitable trade-off between performance and accuracy. Several strategies can be employed in the CNN domain to address the challenges. Quantisation-Aware Training (QAT) and mixed-precision training enable the model to adapt to lower precision representations during training, reducing accuracy loss during inference with quantised weights. Additionally, selective downsampling and kernel size reduction of CNN architectures help retain relevant information and preserve accuracy. Channel pruning can further offset accuracy loss by removing redundant or less critical channels. As a result, employing these strategies and considering hardware constraints makes it possible to strike an optimal balance between accuracy and performance, unlocking the full potential of efficient applications.

On the other hand, the drawback of traditional libraries and compilers is that they often struggle to keep pace with the rapid development of deep learning (DL) models, leading to sub-optimal utilisation of specialised accelerators. To address the limitation, adopting optimisation-aware domain-specific languages, frameworks, and compilers is a potential solution to cater to the unique characteristics of domain algorithms (e.g., machine learning or image processing). These tool-chains would enable algorithms to be automatically fine-tuned, alleviating the burden of manual domain-specific optimisation.

Image Processing Algorithms on Heterogeneous Platforms

Feature extraction algorithms and Convolutional Neural Networks (CNN) are widely used in various problem domains, such as object detection, image classification, and segmentation. Feature Extraction are typically designed to identify and extract relevant patterns or features from the input data. These algorithms are typically designed and implemented on DSPs or GPUs, which offer a specialised architecture properties which include thousands of general compute cores and coupled with a large amount of high-bandwidth memory.

In the case of CNNs that contain millions of parameters, which in turn require significant memory resources to store their weights, implementing them on low-resource and energy constrained platforms is limited. Heterogeneous platforms solves these constraints by utilising various specialised processors, such as CPUs, GPUs, TPUs, and FPGAs, to process specific operations. Leveraging the advantages of true heterogeneous architectures, run-time and power efficient designs can be realised by exploiting architectures with sufficient resource and processing capacity.

However, partitioning algorithms remain an arduous task, particularly wh-en distributing operations among various accelerators within heterogeneous architectures. This process necessitates a delicate balance, taking into account critical factors such as computational power, memory bandwidth, and communication overhead. Furthermore scheduling tasks presents its own set of challenges. Scheduling involves determining the order in which tasks are executed on different processing units, considering factors such as task dependencies, resource availability, and load balancing. Therefore, a scheduler is required for managing hardware resources efficiently, controlling concurrency, balancing workloads, prioritising tasks while adapting to dynamic conditions. Thus, the scheduler plays a critical role in orchestrating task execution to minimise data transfers and optimise overall system performance

The important contributions of this chapter is the development of a heterogeneous hardware and adaption of algorithms on that hardware. Starting with an extensive analysis of popular feature extraction algorithms such as SIFT and two CNN architectures, namely ResNet18[154] and MobilnetV2[155]. The feasibility of implementing these algorithms and networks onto heterogeneous systems is investigated by identifying the optimal stage in each network/algorithm to be mapped onto a specific accelerator. A comprehensive benchmarking analysis of the CNNs and SIFT is conducted by performing image classification and feature extraction on a wide range of platforms to discern the layers or stages that exhibit the highest energy consumption, inference, and total runtime. Two new heterogeneous platforms are constructed, one comprising high-performance accelerators and the other an embedded system with power-optimised processors. The algorithms and networks are implemented on both platforms using a fine-grained partitioning strategy and evaluated. Heterogeneous results are compared to the homogeneous accelerator counterparts to determine the best-performing architecture.

The main contributions of this chapter are as follows:

Efficient deployment of CNNs and SIFT, which are computationally faster and consume less energy, is proposed.

Partitioning methods on heterogeneous architectures are introduced by studying the features of CNNs and stages of SIFT to identify characteristics used to determine a suitable accelerator.

Two heterogeneous platforms consisting of two configurations, high-performance and a power-optimised embedded system, are developed.

Development of a heterogeneous scheduler to allocate tasks onto the suitable accelerator.

Benchmarking and evaluating runtime, energy, and inference metrics of popular convolution neural networks and SIFT on a wide range of processing architectures and heterogeneous systems.

Heterogeneous Architecture

In order to implement CNNs efficiently on heterogeneous platforms, A development flow is proposed, shown in Fig. 6.1. The framework identifies the properties of networks and further profiles in accordance with their hardware suitability. Finally, optimise and evaluate the partitioning decisions.

CNN Development Flow:

Network Feature Extraction & Layer Profiling Analysis

Analysing the network architecture is essential in understanding the role of each layer and how they contribute to the overall performance of the model. This is accomplished by running the CNN on various hardware architectures and profiling the execution time and energy consumption of each layer. Once the resource-intensive layers have been identified by profiling, they can be deconstructed into the types of operations they perform. This deconstruction allows for a more granular understanding of the computational requirements.

Partitioning & Optimisation

To efficiently map operations onto hardware, understanding the instruction sets and memory models of different accelerators is necessary. For example, GPUs excel at performing matrix multiplication during high occupancy, while FPGAs are more power and runtime efficient for smaller matrix sizes. CPUs, with their high clock frequency and memory hierarchy, can be advantageous for sequential layers. Optimisations such as quantisation, pruning, and compression can improve performance, but the trade-offs must be carefully considered.

Performance Evaluation

To determine performance, partitioning strategies and hardware choices are benchmarked using various metrics, such as energy consumption, accuracy, inference, and throughput. Evaluating algorithms not only serves as a comparison to other architecture but also identifies areas for improvement.

The following sections, presents an overview of the representative feature extraction and CNN algorithms targeted for partitioning and implementation on heterogeneous platforms.

Scale-Invariant Feature Transform

The Scale-Invariant Feature Transform (SIFT) algorithm used to detect and describe local features in images. The SIFT algorithm is designed to be robust to changes in scale, rotation, and partial occlusion. It works in several stages: First, it identifies key points in the image through scale-space extrema detection. These keypoints are then localised more accurately and assigned an orientation. Finally, a descriptor is computed for each keypoint, capturing its local image gradient patterns. These descriptors are used for matching keypoints across different images, making SIFT useful for tasks like object recognition, image stitching, and 3D reconstruction. The in-depth algorithm and its operations are explored in the previous chapter, section 5.2.

SIFT Algorithm Analysis

There are several key stages in the SIFT algorithm that vary in computational complexities and hardware implications. This section discusses the complexity, memory footprint and impact of operations on CPU/GPU/FPGA hardware. The full algorithmic description of SIFT is described in Section 5.2.

Gaussian Pyramid Construction:

The Gaussian stage of the SIFT algorithm poses a considerable computational load on hardware, not only due to the intensive convolution operations but also because of the memory requirements involved. The process of generating multiple intermediate images, each corresponding to a different scale, can lead to significant memory consumption, particularly for high-resolution images. For a square image with dimensions of N x N, the complexity of the convolution operation grows quadratically with N, resulting in a substantial computational load. This process is repeated for each of the K scales, further adding to the overall computational demand. Moreover, the hardware would require high memory bandwidth for accessing large filter kernels and image matrices. In addition to the computational complexity, the memory footprint of storing multiple Gaussian-filtered images can become a bottleneck, especially when dealing with large images or a high number of scales. Architectures with higher parallelisation and memory caches are more suitable for this stage.

Extrema Detection:

The computation required to determine these extrema involves a pixel-by-pixel comparison, evaluating whether each pixel qualifies as an extremum. While this comparison is conducted for every pixel in the image. These are \(O(1)\) operations for each pixel, and given the nature of the operation, lower compute resources are required. The extrema detection algorithm operates independently on each scale level of the pyramid, comparing pixels within a local neighbourhood to identify potential keypoints. Therefore, this stage can be implemented in parallel which maps well to GPUs and FPGAs.

Orientation and Magnitude Assignment

While square root and arc tangent operations are less computationally intensive compared to convolutions, they still pose a significant computational burden, especially when performed on a large number of pixels. Hardware support for fixed-point or floating-point arithmetic can significantly accelerate these calculations, as these specialised units are optimised for handling complex mathematical operations.

Descriptor Generation:

In the histogram binning and normalization stage of SIFT, local image gradients are quantised into orientation histograms and then normalised to enhance the robustness of feature descriptors. Binning involves multiplication and addition operations while normalisation involves division which requires more resource logic on hardware. However, the operation intensity is relatively lower than the previous stages which makes it suitable for all architectures.

Experimental Design

The selected profiling times for each stage and on each hardware are shown in Fig. 6.2. The runtime profiles of each SIFT stage were collected using a robust experimental methodology. The input is a greyscale \(3840 \times 2160\) resolution image. The CPU and GPU implementations leveraged the OpenCV SIFT function, while the FPGA was developed using Verilog. The CPU and GPU code is executed 1000 times, and its runtimes are averaged. In the FPGA implementation, the resulting timing graphs from the simulations are used to determine the time taken for each stage. All architectures had 16-bit float precision for their respective designs and algorithms.

SIFT Profiling & Partitioning Strategy

The results reveal that the CPU is substantially slower in execution time than GPU and FPGA by \(2\times\) on average. Even though the CPU has the highest clock speed, the lack of many processing cores results in poor for-loop unrolling optimisations for parallelisation. Comparing only GPU and FPGA, the overall Total runtime has shown the GPU being \(0.83 \times\) faster. In the Gaussian Pyramid and Orientation & Magnitude stage, the GPU outperforms the FPGA by \(2 \times\). On the other hand, the FPGA outperforms the GPU in the Extrema Detect stage by \(1.5 \times\). The GPU and FPGA architectures are comparable in performance when generating keypoint descriptors due to a lower amount of operations. Overall, the lower GPU runtime in most stages is attributed to having a significantly higher clock speed (e.g., 1725MHz vs 300MHz) and more processing cores than the FPGA to maximise throughput.

The partitioning strategy shown in Fig. 6.3, focuses on striking a balance between potential energy consumption and the execution time of the heterogeneous platform.

The RGB to greyscale conversion is a computationally lightweight image processing operation. It involves a linear combination of the red, green, and blue colour channels with specific weightings to produce a greyscale image. The decision to execute rgb2gray algorithm on the CPU instead of the GPU or FPGA is due to minimising the overhead associated with transferring the image data. Although GPUs and FPGAs can perform the RGB to Gray conversion slightly faster due to their throughput processing and pipelining capabilities, the time spent moving the data to and from these platforms can negate the benefits, especially for smaller image sizes where the conversion isn’t the bottleneck.

The "Gaussian Pyramid" executed on GPU is faster than the CPU and FPGA since the vast number of cores and memory resources available can utilise majority of the matrix multiplication operations. To create these scale-space representations, the algorithm needs to access the image data repeatedly for each scale level. The Gaussian filters, used to perform blurring, have larger kernels (in terms of memory requirements) as the scale level increases. Additionally, the image data must be read from memory for each scale level, leading to significant memory access. This heavy memory access is due to the repetitive application of convolution operations with Gaussian filters at multiple scales. The memory bandwidth and efficiency become critical in this stage, especially when working with large images or implementing the algorithm on hardware platforms. Therefore, GPUs can provide an advantage in scenarios where larger memory bandwidth is needed over FPGAs. The "Extrema Detection" is allocated to GPU to reduce additional data transfer costs that would offset any performance gain. The "Orientation & Magnitude" operations are better suited to the FPGA due to the customised pipelining offered, which allows a higher number of gradient calculation operations per clock cycle. In the final operation stage, "Descriptor Generation", the FPGA offers comparable performance to the GPU while consuming less energy per operation and reducing additional data transfers.

Convolutional Neural Network

This section describes the architecture of two widely used CNNs, Resnet18 and MobilenetV2. Each CNN is profiled layer by layer and a partitioning strategy is developed to execute on the heterogeneous platform. The layer characteristics and profiling results support the partitioning methods.

Convolution Neural Network Architecture:

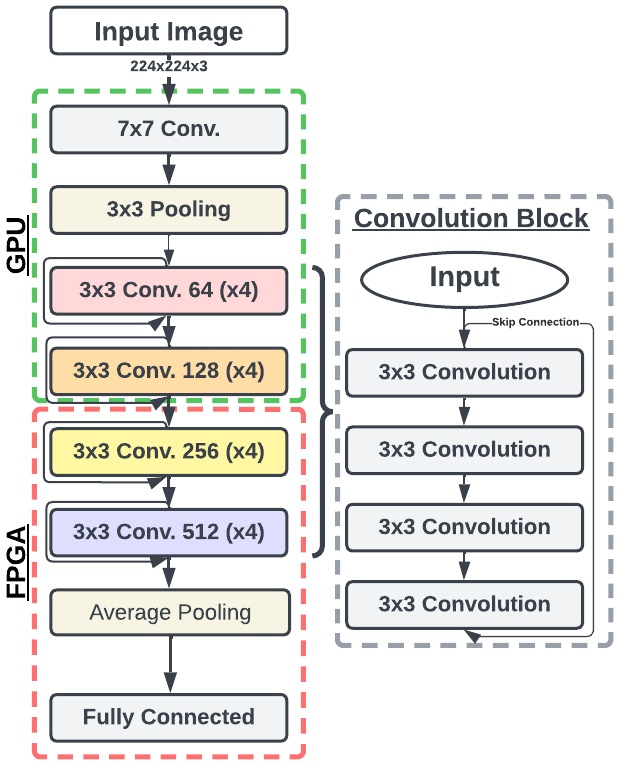
ResNet-18: is a deep convolutional neural network architecture observed in 6.4, that employs several key techniques to achieve state-of-the-art performance in various computer vision tasks. Its design is driven by the need to train very deep neural networks while mitigating issues like vanishing gradients. The key components and technical details of ResNet-18 are as follows:

Convolutional Layers: ResNet-18 comprises a total of 18 layers, which are organised into several stages. The first layer is a \(7\times7\) convolutional layer with a stride of 2. This layer is followed by a max-pooling operation with a \(3\times3\) window and a stride of 2. The large kernel size in the initial layer helps capture larger spatial features.

Batch Normalisation and ReLU Activation: After each convolutional layer, batch normalisation is applied to stabilise and accelerate training. This is followed by the Rectified Linear Unit (ReLU) activation function, which introduces non-linearity into the network. The combination of batch normalisation and ReLU helps in faster convergence and regularisation.

Residual Connections: One of the distinctive features of ResNet-18 is its use of residual connections. These connections introduce identity mappings, which allow the network to learn the residual information between layers. Mathematically, the output of a residual block is calculated as follows: \[F(x) = \mathcal{H}(x) + x\] Where \(x\) is the input to the block, \(\mathcal{H}(x)\) represents the transformation applied by the block, and \(F(x)\) is the output.

Downsampling Blocks: Each stage in ResNet-18 contains multiple residual blocks. After a series of convolutional layers within a stage, a downsampling block is applied. The downsampling block typically involves a convolutional layer with a stride of 2, which reduces the spatial size of the feature maps while increasing the number of channels. This operation effectively reduces the computational burden while preserving important information.

Softmax Classification Layer: The final layer of ResNet-18 is a softmax classification layer. It takes the feature map produced by the preceding layers and computes a probability distribution over output classes. The softmax function is applied to the features, and the resulting probabilities indicate the likelihood of the input belonging to different classes.

Shortcut Connections: To prevent vanishing gradients and facilitate the flow of information, shortcut connections are introduced in residual blocks. These connections skip the first two convolutions within a block and add the input directly to the output of the third convolutional layer. This way, the gradient can flow backwards through the skip connection, making it easier to train very deep networks.

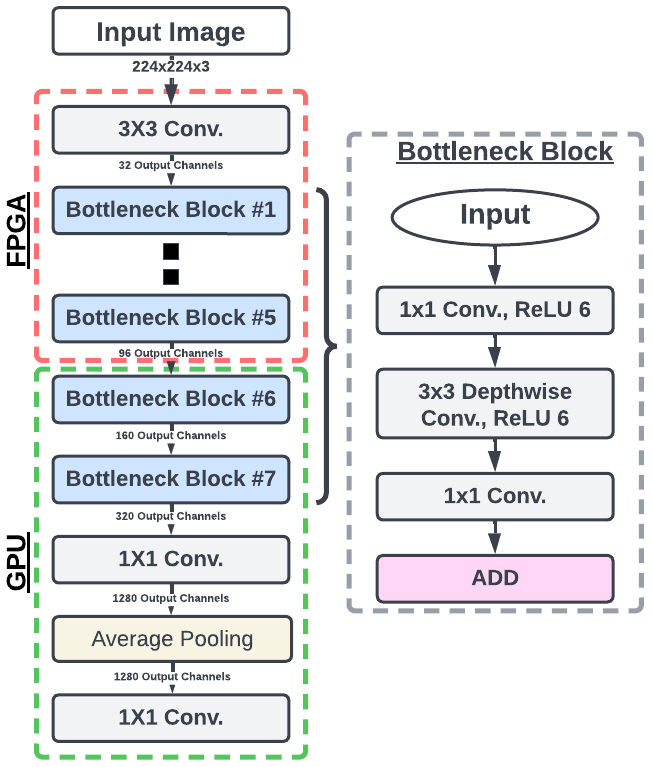
MobileNetV2: shown in 6.5, is an embedded-optimised convolutional neural network architecture that uses a range of techniques to achieve high accuracy with low computational cost. Key details of MobileNetV2 include:

Depthwise Separable Convolution: MobileNetV2 employs a depthwise separable convolution technique. It divides a standard convolution operation into two distinct steps: depthwise convolution and pointwise convolution. Depthwise convolution first performs a separate convolution for each input channel using a kernel of size \((k, k)\), where \(k\) is the filter size. This reduces the computational load by a significant margin.

The depthwise convolution operation is computed using Eq. ([eq:depthwise]):

\[\label{eq:depthwise} y = \text{depthwise\_conv}(x, W_{d})\]

where \(y\) is the output, \(x\) is the input feature map, and \(W_{d}\) are the depthwise convolution weights.

Pointwise Convolution: After the depthwise convolution, pointwise convolution is applied using \(1\times1\) kernels. Pointwise convolution combines the results of the depthwise convolution by performing a linear combination of the channels. This step helps to capture complex relationships between channels and is critical for maintaining model accuracy.

The pointwise convolution operation shown in  Eq. ([eq:Pointwise]):

\[\label{eq:Pointwise} y = \text{pointwise\_conv}(x, W_{p})\]

where \(y\) is the output, \(x\) is the result of the depthwise convolution, and \(W_{p}\) are the pointwise convolution weights.

Reduction of Computational Cost and Parameters: The combination of depthwise separable convolution reduces the computational cost significantly, making MobileNetV2 suitable for resource-constrained embedded devices. The reduction in the number of parameters and the computational requirements is a crucial advantage.

Linear Bottlenecks: MobileNetV2 also introduces linear bottlenecks, which are inexpensive \(1\times1\) convolutions placed between a ReLU activation function and a \(3\times3\) convolution. These linear bottlenecks are designed to keep the computational cost low while ensuring that the network maintains a high level of accuracy. The ReLU activation helps introduce non-linearity, while the subsequent \(3\times3\) convolution captures more complex features.

The linear bottleneck operation represented in  Eq. ([eq:bottleneck]):

\[\label{eq:bottleneck} y = \text{conv\_3x3}(\text{ReLU}(\text{conv\_1x1}(x, W_{l})), W_{3x3})\]

where \(y\) is the output, \(x\) is the input, \(W_{l}\) are the linear bottleneck weights, and \(W_{3x3}\) are the weights for the \(3\times3\) convolution.

CNN Profiling & Partitioning Strategy:

In this section, both CNN architectures are analysed and partitioned onto the appropriate accelerator based on their runtime profiles. The CNN hardware comparison results are displayed in Figure Fig. 6.6 & Fig. 6.7.

Experimental Design

The runtime profiles of each CNN architecture layer were collected using a robust experimental design. Both MobileNetV2 and ResNet18 architectures used a \(3840 \times 2160\) resolution image dataset. The CPU and GPU implementations leveraged the Pytorch library and its CUDA configuration. A custom hook function was defined to measure the runtime of each convolutional and linear layer during forward pass execution. For every convolutional and linear layer in the model, the hook function recorded the start and end times, allowing calculation of the layer-wise runtime. Through 1000 code execution iterations, the runtimes collected are averaged. In the FPGA implementation, Xilinx deep learning processing unit IP and their resulting timing graphs are used to determine the time taken by each layer. All architectures had 8-bit precision for both models and implementation.

Resnet18:

The Resnet18 results in Fig. 6.6 show the fastest hardware for executing the model is the GPU, with the total execution time of \(0.18\)s, while the slowest is the CPU with \(0.29\)s. The FPGA’s total execution time is between the two with \(0.19\)s.

The conv1 layer is computationally intensive for all platforms as it applies 64 filters of size \(7\times7\) to a large input image with multiple colour channels. This results in a large number of multiply-accumulate (MAC) operations. The conv1 layer also performs padding and activation functions, which adds to the overall computational cost. However, the execution time for Conv1 is significantly faster on the GPU, which can parallelise the computations across multiple cores. In layers \(L1\sim L2\), the GPU is \(1.36\times\) and \(1.10\times\) faster than the FPGA. Therefore, the GPU is the best candidate to allocate Conv1, L1 and L2 for execution.

The \(L3\sim L4\) and Fully Connected (FC) layers take relatively less time to execute. The size of feature maps decreases as they progress through the layers due to downsampling operations like pooling and strides. The \(L3\sim L4\) convolutional and average pool layers can be executed on the FPGA since fewer MAC operations are occurring for the GPU to be fully utilised while taking advantage of power efficient architecture.

MobilenetV2:

The Fig. 6.7 results show that the total execution time for the CNN on the CPU was \(0.241\)s, while on the GPU and the FPGA, it was \(0.23\)s and \(0.20\)s, respectively. The bottleneck layer with the longest execution time for all three devices was BN1, with a time of \(0.02202\)ms on the CPU, \(0.015\)ms on the 3070 GPU, and \(0.0034\)ms on the FPGA.

The runtime for each bottleneck layer decreases as it moves from Bottleneck 1 to Bottleneck 7 due to reduced input channels and the amount of computation required to process the data in each layer. Thus, the later bottleneck layers take less time to execute than the earlier ones. The first five bottleneck layers are suitable for execution on the FPGA, as it shows that it performs \(\sim4\times\) faster than the GPU on average. The reason behind the faster execution on FPGA can attributed to multiple factors below:

Direct, custom and optimised routing between logic allows efficient data-flow transfer and locality.

Separable filters and feature maps have reduced memory footprint which can be efficiently managed.

Efficient use of pipelining for convolutional operations and reduced data dependency (e.g., ResNet18 residual connections).

The remaining Bottleneck 5 \(\sim 7\) layers are suitable for execution on the GPU because of a slight performance advantage and shorter initialisation transfer time back to the host. The Softmax and fully connected layers are also computed on the GPU since the performance is comparable to the FPGA and reduces data transfer overhead. Both layers are required to transform features into a suitable format, and it assigns a probability score for classification.

Experimental Setup

This section introduces both heterogeneous implementations and their corresponding tools and software used to target those architectures. In addition, a detailed break of the scheduler used to move data between all accelerators while keeping tasks synchronised. Both power and execution time are discussed in detail which are used to evaluate both platforms.The proposed partitioning is tested using two developed heterogeneous platforms containing high-low power components, as shown in Table [tab:HWEnvironment], and described below:

(a)	(b)

Low-Power System: The constructed system consists of a custom carrier board which is equipped with several key components, including an Artix-7 (XC7A200T) FPGA, a Jetson Xavier NX, and an ARM CPU. To provide additional storage space, the Linux image is flashed onto the SD card rather than the 16Gb eMMC. Communication between the FPGA and the Xavier NX is achieved through a PCIe gen2 4-lane interface, which is connected via an M.2 key-M connector.

High-Power System: The system consists of CPU (AMD 5900x), GPU (GTX 3070) and FPGA (Xilinx ZCU106), integrated into a desktop with 32GB 3200Mhz DDR4 Memory. Both devices are interfaced via PCIe Gen3 and the communication to the host CPU uses direct memory access (DMA), allowing the movement of data between host memory and subsystems. The GPU and FPGA drivers are used to program the DMA engine and DMA/bridge subsystem IP. Idle CPU is frequency scaled to reduce power consumption.

Dataset. The test images used in the experiments are from LIU4K-v2 dataset [153], which is a high resolution data-set that includes 2000 \(3840\times2160\) images. The images contain a variety of backgrounds and objects.

Heterogeneous Scheduler Architecture

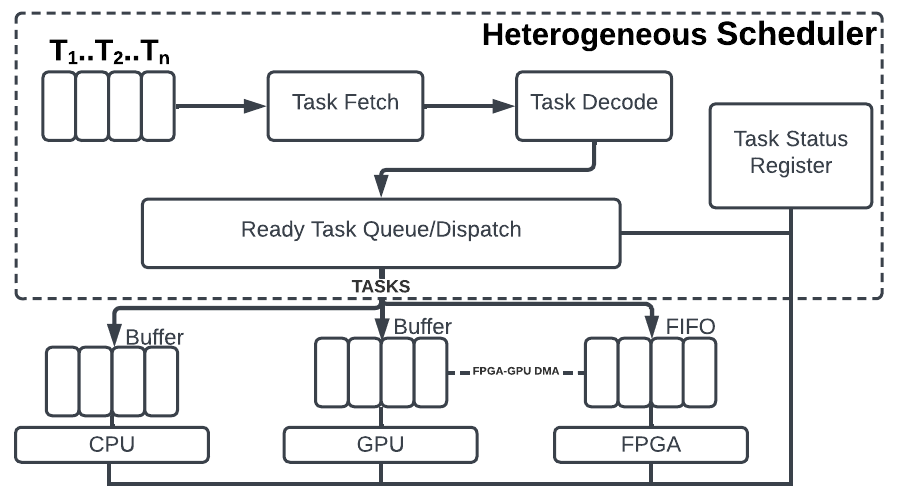
A heterogeneous scheduler architecture in Fig. 6.9 is developed, which is responsible for distributing and managing tasks or workloads across different types of processing units or resources. The scheduler is written in C/C++ to manage memory transfers and pass the feature map and operation stage data from the CPU and into the GPU or FPGA.

The scheduler uses a First-Come, First-Served (FCFS) algorithm due to its relatively simple construction and minimal runtime overhead. The operation stages in imaging algorithms are executed sequentially. Therefore, tasks are partitioned in order based on their dependency on previous task data, which makes it suitable for this type of scheduling algorithm. The pre-partitioned ordered tasks are fetched from the queue and decoded to prepare for execution. As tasks are dequeued, they are placed in the task ready queue, a staging area where tasks await execution. The task ready queue ensures that tasks are readily available for the execution stage. Each task contains a predefined pragma which tells the scheduler which architecture to execute the operation on. Additionally, a task status register is used to keep track of the current state and progress of each task. This register provides real-time information about the task’s status, whether it is waiting, executing, or completed. The task status register is essential for maintaining task synchronisation and ensuring that tasks progress through the execution pipeline smoothly. It allows the scheduler to monitor and manage the execution of tasks and make informed decisions based on the tasks’ statuses, ensuring optimal resource utilisation and order of execution.

The pseudocode presented in Algorithm [Alg:HeterogeneousScheduler] outlines the process of the Heterogeneous Scheduler. This algorithm iterates over the tasks in the workload and employs an FCFS queue to execute tasks in the order they were received. The algorithm initialises two functions, ExecuteOnFPGA() and ExecuteOnGPU(), which are used to execute the task on a certain device based on a partitioning strategy. The FCFS queue ensures that tasks are executed in the order of arrival, maintaining fairness and accuracy in task execution. Once all tasks have been executed, the algorithm transfers the output data from the FPGA or GPU to the CPU, depending on which device the output is stored on. This transfer facilitates the consolidation of results for further processing. Lastly, the algorithm post-processes the output to generate the final result of the workload.

CPU-GPU-FPGA Data Communication

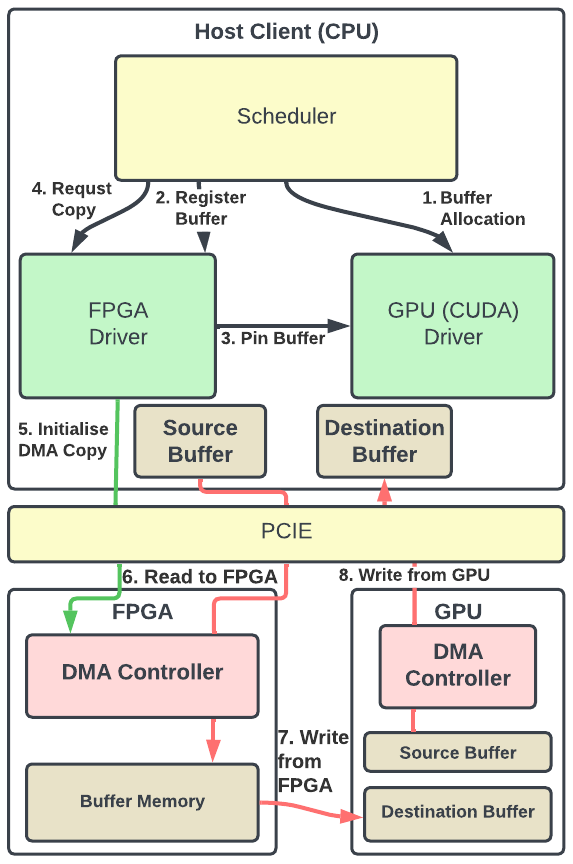
The data transfer process controlled by the scheduler follows a series of steps described below:

Allocate Buffer: Allocate memory buffers on both the GPU and FPGA to hold the data to be transferred.

Register Buffer: Register the GPU buffer with the FPGA using PCIe Base Address Register mapping or GPUDirect Remote Direct Memory Access to enable direct access.

Pin Buffer: Pin the GPU buffer to prevent it from being swapped out of physical memory, ensuring consistent and efficient access by the FPGA/Host.

Request Copy: Initiate the data transfer from the GPU buffer to the FPGA buffer using a Direct Memory Access controller.

Program DMA Copy: Configure the DMA engine’s source and destination addresses, transfer size, and control parameters to transfer data autonomously.

Handle DMA Completion: Monitor the DMA engine’s status flags or interrupts to detect transfer completion.

Process Data on FPGA/GPU: Access the transferred data from the destination buffer.

In the case of FPGA, the scheduler uses the drivers to initialise the DMA to allocate buffer pointers and then pass the pointer to the write function. After receiving the input data and its size, the driver creates a descriptor and initialises the DMA process by providing the descriptor’s start address. The driver writes a control register to start the DMA transfer, which reads the descriptor and fetches the feature map data to be processed on the FPGA.

On the GPU side, the CPU host code allocates device pointers using CUDA functions like cudaMalloc to specify the locations in the GPU’s memory where the data will be placed. Then, the CPU host code invokes CUDA API functions such as cudaMemcpy to request the data transfer. The GPU driver, which manages GPU resources, sets up the transfer, allocates GPU memory, and configures the data transfer channels. It ensures that the FPGA’s memory is correctly mapped to the GPU’s address space to enable efficient transfer. Subsequently, the GPU driver issues commands to the GPU to initiate the data transfer. The actual transfer is executed by the GPU hardware using Direct Memory Access (DMA). Once completed, the GPU returns a status to the driver. The CPU host code can then access and process the data in the GPU’s memory. Synchronisation mechanisms, like CUDA events or cudaStreamSynchronize, may be employed to ensure that the GPU doesn’t process the data prematurely.

The systems exploit GPUDirect RDMA shown in Fig. 6.10 to facilitate low-latency communication without involving the host CPU by retrieving the bus address of buffers in GPU memory. Traditionally, BAR windows are mapped to the CPU’s address space using memory-mapped I/O (MMIO) addresses. However, current operating systems lack mechanisms for sharing MMIO regions between drivers. Therefore, the NVIDIA kernel driver provides functions to handle address translations and mappings. This means that data can be moved directly between the GPU and the host without the need for intermediate buffers or copies in CPU memory. This approach significantly improves data transfer efficiency, particularly for large images or data, as it eliminates unnecessary data movement and reduces memory overhead.

Execution time

The evaluation of the overall system performance considers both latency and compute factors, reporting performance metrics for total time, inference, and other significant layers while using floating point 16 precision. Other devices, such as i9-11900KF (5.30GHz), are also benchmarked for additional insight. The run-time is measured using the host platform’s built-in time libraries. The network performance is estimated by executing and averaging the results of 100 images. The frame per second (FPS) metric is computed using Eq. [eq:FPS]:

\[\label{eq:FPS} \text{FPS}= 1/\text{Execution Time}.\]

Power Consumption

(a)	(b)

Two common methods used for measuring power are software and hardware based. Accurate power estimation is always challenging for software tools because they have to assume various factors in their models. Additionally, Taking the instantaneous power or TDP of a device is not accurate since power consumption varies on the specific workload. Therefore, measuring power over the time it takes for the algorithm to execute improves accuracy as opposed to using just fixed Wattage. The hardware measurement approach uses a current clamp meter shown in 6.11, which outputs a voltage for every Amp measured. The Otii Arc Pro[156] data-logger captures the time series data from the current clamp and generates a graph showing the current consumption over time. A script is developed to start and stop the measurements during the algorithm’s execution. The mean current is averaged and multiplied by the input voltage to determine the energy consumed in Joules (J).

The energy consumption is obtained using Eq. ([eq:Energy]) where E is energy, P represents power and t time.

\[\label{eq:Energy} E = P \times t\]

Experimental Results

In this section, results of both CNN and SIFT algorithms implemented on a heterogeneous platform are observed and discussed in-depth.

Heterogeneous SIFT Results

In achieving that, a custom pipeline was created by targeting various algorithm components on different hardware based on their suitability obtained from the benchmarking framework. This includes the latency of transferring image data between memory and the accelerators. The heterogeneous architecture empowers the ability to pick and execute operations within the image processing algorithms on each architecture to meet the speed and power target. However, within the scope of this work, only an initial configuration of the SIFT algorithm is reported, which establishes preliminary steps toward future work on finding the most optimal configuration for the algorithms.

Heterogeneous SIFT Runtime & Energy Consumption

Table [tab:heterogenoussummary] shows the execution time of the SIFT algorithm on a heterogeneous platform. The table includes memory transfer latency between the host and devices, an aspect frequently overlooked in similar analyses. The results reveal that the heterogeneous platform (Excl. Memory Transfer) outperforms all discrete architectures, CPU, GPU and FPGA by \(103\times\), \(1.21\times\) and \(1.43\times\), respectively. However, taking data transfer into account, the heterogeneous architecture increases in execution time due to host task scheduling. On the other hand, As accelerators are fabricated on the same silicon die, memory latency would significantly be reduced.

The energy consumption results in Fig. 6.12 reveal that the CPU consumes the most energy for all operation stages in SIFT and RGB2Gray while the FPGA used the least. The Gaussian Pyramid stage stands out as the most energy intensive due to the substantial number of operations it requires. In contrast, the low resource requirements of RGB2Gray and Descriptor Generation stages reflected lower energy usage.

The heterogeneous architecture, which combines CPU, GPU and FPGA resources, strikes a balance between power consumption and execution time. The "Total" power consumption is notably lower than the CPU but between both GPU and FPGA since the static power of other accelerators is taken into account.

Heterogeneous CNN Results

The results in Fig. 6.14 & Fig. 6.15 show the total run-time and energy consumption of Resnet18 and MobilenetV2 on each architecture and heterogeneous platform while Fig. 6.13 shows the inference in Frames per Second. The tables [tab:Mobilenet-V2 Result Summary] & [tab:ResNet-18 Result Summary], summarises the results for the Total Execution Time, Inference, Convolution, Fully Connected, Total Energy, CPU Energy, Device Energy & Datalogger

Inference

According to Fig. 6.13, Resnet18 CNN had the highest FPS value at \(270\) in contrast to MobileNetV2 \(243\) FPS on high and low power heterogeneous architecture. This difference in FPS can be attributed to the network depths and parameters, with ResNet-18 having \(18\) layers and MobileNetV2 having \(53\) layers, leading to differences in computational complexity. Considering individual hardware only, the ’3070’ GPU achieved the highest FPS on Resenet18 and the ’ZCU106’ FPGA for MobileNetv2. On the other hand, the Artix-7 has the lowest FPS in both architectures due to limited resources and clock speed. In the case of both heterogeneous systems, HP & LP architectures achieve higher FPS than their individual counterparts.

Total Execution Time

Regarding Fig. 6.14 for Resnet18, it can be observed that the Artix-7 exhibits the highest total execution time, taking approximately \(1.1\) seconds to complete the task. Conversely, the ’GPU: 3070’ has the lowest real execution time, both completing the task at approximately \(0.18\)s. As for MobileNetV2 in 6.15, the ’FPGA: Artix-7’ platform also leads with the highest execution time at \(1.4\)s, while the ZCU102 classifies the image in \(0.19\)s and GPU at \(0.23\)s. It is noteworthy to mention that the higher runtimes observed for the GPUs may be attributed to the communication and transfer of data from the CPU and lower core utilisation.

Total Execution time speedups of high (HP) and Low (LP) power systems are compared against their fastest discrete components within each system. The ’HP’ system demonstrated a speedup of \(1.05\times\) over the ’GPU:3070’ for Resnet18 and \(1.05\times\) forMobileNetv2. In the case for ’LP’ system, it exhibited a speedup of \(1.21\times\) over the ’GPU: Xavier NX’ for Resnet18 and \(1.06\times\) for MobileNetv2. The Convolution layer results show that the most time is spent performing convolution operations. However, taking in account data/memory transfer latency, both heterogeneous architectures implementations have interconnect (PCIe) and distance bottlenecks. This bottleneck reduces the FPS of HP & LP systems by \(10 \sim 25\) which in turn allows the ’GPU:3070’ to marginally edge out on the HP system. The disparity between the Total Wallclock and Inference runtimes are due to the overhead and initialisation time which include model/weight loading and data preprocessing. In addition, the Fully Connected layer revealed that all architecture had comparable performance due to the layer’s simple MAC operations.

Energy Consumption

Concerning energy consumption, the discrete ’5900 & I9’ CPUs consume the most energy in both CNN architectures, around \(20\sim26\) Joules. The least amount of energy consumed is from both FPGA architectures, ’FPGA: Artix’ and ’FPGA: ZCU106’, which used less than \(15\) Joules for both networks. Taking CPU idle energy usage into account results in GPUs having comparable energy usage statistics with both CPUs which is linked to higher CPU-GPU data transfer and initialisation cost. However, HP and LP systems consume \(1.02\times\) and \(1.03\times\) less energy, respectively, compared to the single ZCU106 and Artix architectures for Resnet18. As for MobileNetV2, there is a \(1.06\times\) and \(1.07\times\) reduction in energy consumption for the ’HP’ and ’LP’ systems, respectively. The idle accelerators within heterogeneous systems had their clocks lowered to save on static energy consumption. However, a small increase in idle energy usage was observed during execution. If idle energy is taken into account, then the energy consumption results of both HP & LP systems would be greater than discrete FPGA but lower than GPU.

Conclusion

In this chapter, partitioning strategies are introduced to map the layers of two widely used convolutional neural networks, namely, Resnet18 and Mobilnetv2, along with a feature extraction algorithm (SIFT), onto a heterogeneous architecture. Two new CPU-GPU-FPGA systems, one designed for high performance and the other for low-power consumption, are proposed. The experiments demonstrate that when layer/per-operation partitioning methods are applied, both high-power and low-power systems outperform homogeneous accelerators in terms of energy efficiency and execution time. Furthermore, the results suggest that partitioning networks based on their layer profiles holds the potential for efficient deployment on heterogeneous architectures, offering a viable alternative to GPU/FPGA-only applications.

Discussion, Conclusions and Future Work

The aim of this thesis is to present domain-specific optimisation techniques for image processing algorithms on heterogeneous hardware. In section 7.1, the research problems are identified and discussed. Furthermore, in section 7.2, the contributions to addressing the problems are presented. Lastly, in section 7.3, future research directions extending the work are suggested.

Discussion

The thesis focuses on achieving two main research aims, "Which is the best method of partitioning and implementing algorithms on heterogeneous hardware" and "Identifying domain-specific optimisations and understanding the performance and accuracy trade-offs".

In the case of implementing algorithms on heterogeneous platforms, the primary challenge is navigating the route to hardware. Designers often face a complex terrain of diverse hardware architectures, each with unique constraints and optimisation opportunities. This problem can lead to a time consuming and error-prone process of manually configuring and optimising algorithms for specific accelerators. Moreover, the need for standardised tools and interfaces across platforms further exacerbates the difficulty of seamless integration. Designers must grapple with the intricacies of synchronisation and resource allocation, which can be particularly daunting in complex, real-time image processing applications. These challenges underscore the need for a more streamlined and systematic approach to ensure efficient deployment of algorithms on heterogeneous platforms.

The other challenge for heterogeneous systems is efficiently managing data transfers between various processing units. Data movement between processors introduces latency and consumes substantial computational resources and memory bandwidth. In image processing, operations usually form a pipeline often subject to data dependencies, making it difficult to optimise the scheduling of tasks. Therefore, inefficient data transfers can lead to a significant performance bottleneck.

Optimisation is an essential step towards extracting the best performance out of systems. Traditional optimisations are not domain-aware and, therefore, cannot exploit the unique properties of specific problem domains to improve performance. Additionally, understanding the trade-offs between domain-specific optimisations and energy consumption or accuracy has not been fully considered.

Finally, implementing deep-learning algorithms such as CNNs or feature extraction algorithms on heterogeneous architectures necessitates the development of fine-grained partitioning strategies. Applying these strategies requires a thorough understanding of hardware architectures and profiling. In addition, developed metrics should be used to effectively evaluate the performance of heterogeneous implementations based on the type of algorithm deployed. Addressing these challenges is critical to unlocking the full potential of heterogeneous architectures.

Conclusions

To achieve the first objective of efficient deployment of algorithms on heterogeneous platforms, the characteristics of image processing algorithms were decomposed into fundamental operations. A benchmarking framework is presented in Chapter 4 to understand the features of algorithms found in the image-signal pipeline and to determine their suitability for specific accelerators in a heterogeneous environment. This modular framework, termed the Heterogeneous Architecture Benchmarking Framework on Unified Resources (HArBoUR), provides an in-depth analysis and set of metrics for imaging algorithms, which in turn enables the identification of the most efficient processing unit. To support the proposed framework, low and high complexity image processing pipelines are evaluated on each architecture using various tools and libraries. This gives a comprehensive insight into their design choices and optimisations. Different evaluation metrics are proposed such as throughput, energy per operation and clock cycles per operation.

The following chapter 5, explores domain-specific optimisation techniques within image processing. Several optimisations were proposed and validated on CNNs, feature extraction and filter algorithms. The results for CNN and filter algorithms had significantly reduced computation times on all processing architectures. In the case of the optimised SIFT algorithm implementation, it had outperformed the state-of-the-art on FPGAs. Additionally, it achieved runtime at par with GPU performances while consuming less power. However, these optimisations come at the expense of reduced accuracy, highlighting the need for thoughtful consideration when aiming to enhance performance through domain-specific optimisations.

In the concluding Chapter 6, the development of two low and high-power heterogeneous systems using commercial off-the-shelf hardware is discussed. Moreover, two convolutional networks and a feature extraction algorithm are profiled and analysed to identify performance hotspots and assess their hardware compatibility. The algorithms are then partitioned onto the most efficient hardware using a fine-granular strategy, involving the separation of CNNs layer by layer and operations within the feature extraction algorithm. The implemented heterogeneous algorithms are evaluated against their discrete hardware counterparts, resulting in notable speedups in performance and reduced energy consumption.

Limitations & Future work

In this section, the limitations and potential future directions of this research are discussed below:

Heterogeneous Benchmark Framework

The heterogeneous benchmarking framework proposed in Section 4 can be extended by including additional performance metrics that consider communication latency and scheduling of algorithms to determine the true performance. Further developing a tool-chain to support designers by highlighting key areas of code that can be accelerated by a particular processor and automatically partitioning algorithms without requiring additional designer input. This automation not only saves time but also ensures that the resulting code is fine-tuned on the target hardware.

Domain-Specific Optimisations

The methods described in Section 5.1 mainly centre on applying optimisations uniformly across the entire algorithm, resulting in the same optimisation being applied to every operation stage within the algorithms. This coarse-grained approach may potentially impact accuracy while having no significant impact on the overall runtime. Therefore, adopting a fine-grained approach by applying optimisation strategies to specific parts of an algorithm. An example of a granular approach involves applying optimisations to individual layers of a CNN or each stage of the SIFT algorithm, where each operation is fine-tuned independently. Additionally, the development of a domain-specific compiler capable of dynamically adapting and optimising algorithms based on runtime conditions, accuracy requirements, energy considerations, and data patterns can further enhance the efficiency and effectiveness of domain-specific optimisations on a heterogeneous platform.

Heterogeneous Implementations

In section 6, future directions of this chapter involve improving the hardware, scheduler and measurement accuracy. Initially, The heterogeneous scheduler on the high performance system transfers the output of one operation or layer onto the pinned memory of the GPU or buffer. The transfer is indirect since it has to go through the CPU, but can be shortened through direct memory transfer between accelerators. The scheduling algorithm can be improved by dynamically scheduling workloads for image processing if requirements change.

To address the challenges with data transfer latency can be separated into two categories, Hardware and Software listed below:

Hardware: Using a faster interface between accelerators than PCIe or integrating the cores onto a single compute chip to reduce the data transfer distance.

Hardware: Utilising in-memory processing which integrates computation within memory modules. This design reduces data movement overhead and latency by processing data where it’s stored rather than shuttling it between memory and processors.

Software: Latency-aware compilers predict anticipated data usage by different processors and proactively optimise data placement to improve data locality.

Domain-Specific Language

All the previously mentioned future research directions can be unified within the framework of an image processing domain-specific language targeting image processing. The language would allow users to streamline the development of customised image pipelines by mapping algorithms together using a data-flow model. The result of abstracting away from hardware using a high-level signal flow diagram would simplify the route to hardware while removing the burden of partitioning and manual tuning from the designer.